Question

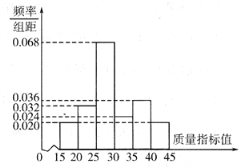
【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会，动员各方力量，迅速全面展开新旧动能转换重大工程．某企业响应号召，对现有设备进行改造，为了分析设备改造前后的效果，现从设备改造前、后生产的大量产品中各抽取了200件作为样本，检测一项质量指标值．若该项质量指标值落在内的产品视为合格品，否则为不合格品．如图所示的是设备改造前样本的频率分布直方图．

（1）若设备改造后样本的该项质量指标值服从正态分布，求改造后样本中不合格品的件数；

（2）完成下面2×2列联表，并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关．

0	设备改造前	设备改造后	合计
合格品件数
不合格品件数
合计

附参考公式和数据：

若，则，．

	0.150	0.100	0.050	0.025	0.010
	2.072	2.706	3.841	5.024	6.635

Answer 1

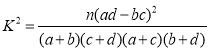
【答案】（1）10；（2）列联表见解析，有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关．

【解析】

（1）设备改造后该项质量指标服从正态分布，得，，然后，然后即可求出

（2）由设备改造前样本的频率分布直方图，可知不合格频数为，然后填表，再算出即可

解：（1）∵设备改造后该项质量指标服从正态分布，

得，，

又∵，

∴设备改造后不合格的样本数为．

（2）由设备改造前样本的频率分布直方图，可知不合格频数为

．

得2×2列联表如下

	设备改造前	设备改造后	合计
合格品	160	190	350
不合格品	40	10	50
合计	200	200	400

，

∴有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关．