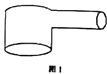
题目内容
【题目】在直三棱柱ABC — A1B1C1中,AB=AC,BB1=BC,点P,Q,R分别是棱BC,CC1,B1C1的中点.
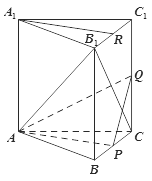
(1)求证:A1R//平面APQ;
(2)求证:直线B1C⊥平面APQ.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)先证明四边形![]() 是平行四边形,然后利用线线平行可证线面平行;
是平行四边形,然后利用线线平行可证线面平行;
(2)先证明![]() ,
,![]() ,结合线面垂直的判定定理可得直线B1C⊥平面APQ.
,结合线面垂直的判定定理可得直线B1C⊥平面APQ.
证明:(1)在直三棱柱![]() 中,
中,![]() 且
且![]() ,
,
因点![]() 分别是棱
分别是棱![]() 的中点,所以
的中点,所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,即
是平行四边形,即![]() 且
且![]() ,
,
又![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
即四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为直三棱柱![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
又因![]() ,所以四边形
,所以四边形![]() 是菱形,所以
是菱形,所以![]() ,
,
又点![]() 分别是棱
分别是棱![]() 的中点,
的中点,
即![]() ,所以
,所以![]() .
.
因为![]() ,点
,点![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() ,
,
由直三棱柱![]() ,知
,知![]() 底面
底面![]() ,即
,即![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]()
![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]()
![]() ,
,
所以![]() 平面
平面![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会,动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前、后生产的大量产品中各抽取了200件作为样本,检测一项质量指标值.若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
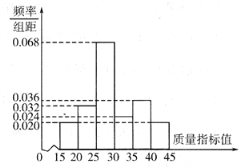
(1)若设备改造后样本的该项质量指标值服从正态分布![]() ,求改造后样本中不合格品的件数;
,求改造后样本中不合格品的件数;
(2)完成下面2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关.
0 | 设备改造前 | 设备改造后 | 合计 |
合格品件数 | |||
不合格品件数 | |||
合计 |
附参考公式和数据:
若![]() ,则
,则![]() ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |