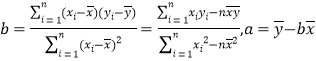题目内容
【题目】已知z0＝2＋2i，|z－z0|＝
.
(1)求复数z在复平面内的对应点的轨迹；
(2)求z为何值时|z|有最小值，并求出|z|的最小值．
【答案】（1）复数z点的轨迹为以z0(2,2)为圆心，
为半径的圆．（2）当z＝1＋i时，|z|min＝
【解析】分析：（1）设
，由
，化简即可得到复数在复平面内对应的点的轨迹；
（2）由（1）可知当复数
点在
的连线上时，
有最大值或最小值，即可得到结果．
详解：(1)设z＝x＋yi(x，y∈R)，由|z－z0|＝
，
得：|x＋yi－(2＋2i)|＝|(x－2)＋(y－2)i|＝，.
解得：(x－2)2＋(y－2)2＝2...
∴复数z点的轨迹为以z0(2,2)为圆心，为半径的圆．..
(2)当z点在Oz0的连线上时，|z|有最大值或最小值..
∵|Oz0|＝2，半径为.
∴当z＝1＋i时，|z|min＝..
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
（1）请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
;
（2）试根据（1）求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式：
