题目内容

| A.R | B.[-9,+ ) ) | C.[-8,1] | D.[-9,1] |
C
解析试题分析:根据题意,由于函数当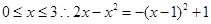 ,开口向下,对称轴x=1,那么结合定义域可知值域的范围是[-3,1],而对于
,开口向下,对称轴x=1,那么结合定义域可知值域的范围是[-3,1],而对于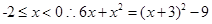 ,同理结合开口方向和对称轴x=-3,可知函数的值域为[-8,0),取各段函数的 值域的并集可知结论为[-8,1],故选C.
,同理结合开口方向和对称轴x=-3,可知函数的值域为[-8,0),取各段函数的 值域的并集可知结论为[-8,1],故选C.
考点:函数的概念
点评:解决的关键是根据已知的二次函数的性质,结合定义域和对称轴来求解各段的最值,再比较得到值域,属于基础题。

练习册系列答案
相关题目
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.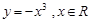 | B. | C. | D.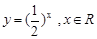 |
已知函数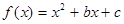 ,且
,且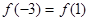 .则( )
.则( )
A.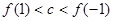 | B.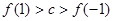 |
C.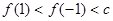 | D.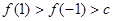 |
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设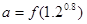 ,
,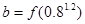 ,
, ,则
,则 、
、 、
、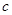 的大小顺序是( )。
的大小顺序是( )。
A. | B.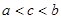 | C. | D. |
函数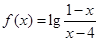 的定义域为( )
的定义域为( )
A.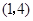 | B.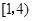 |
C.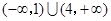 | D.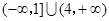 |
设函数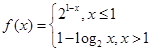 ,则满足
,则满足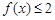 的
的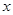 的取值范围是( )
的取值范围是( )
A.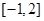 | B.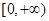 | C. | D.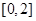 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.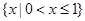 |
 ,若
,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
若定义在R上的偶函数 满足
满足 ,且当
,且当 时,
时, ,则函数
,则函数 的零点的个数为
的零点的个数为
| A.8 | B.6 | C.5 | D.4 |