题目内容
已知函数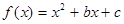 ,且
,且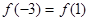 .则( )
.则( )
A.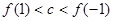 | B.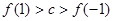 |
C.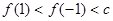 | D.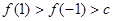 |
B
解析试题分析:∵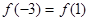 ,∴函数
,∴函数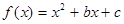 的对称为x=-1,∴函数
的对称为x=-1,∴函数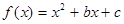 在[-1,+
在[-1,+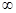 )上单调递增,又1>0>-1,且f(0)=c,∴
)上单调递增,又1>0>-1,且f(0)=c,∴ ,故选B
,故选B
考点:本题考查了函数性质的运用
点评:对于此类问题要掌握题目中式子的转换关系,培养学生灵活运用函数奇偶性与单调性解决问题的能力及创造性

练习册系列答案
相关题目
下列四个数中,其倒数是负整数的是【 】
| A.3 | B.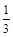 | C.-2 | D.- |
设函数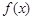
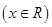 满足
满足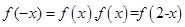 ,且当
,且当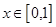 时,
时,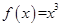 .又函数
.又函数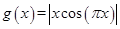 ,则函数
,则函数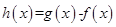 在
在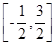 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
定义在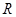 上的奇函数
上的奇函数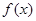 满足
满足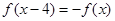 ,且在区间
,且在区间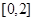 上是增函数,则( )
上是增函数,则( )
A. | B.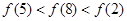 |
C.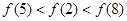 | D.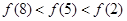 |
定义运算: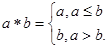 如
如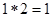 ,则函数
,则函数 的值域为( )
的值域为( )
A.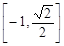 | B.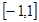 | C.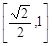 | D.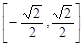 |
已知 上是减函数,那么
上是减函数,那么 ( )
( )
| A.有最小值9 | B.有最大值9 | C.有最小值-9 | D.有最大值-9 |
 上的偶函数
上的偶函数 满足
满足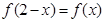 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )
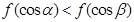
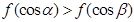
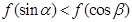
 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( )  B.
B. C.
C. D.
D.

 )
)