题目内容
已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
见证明
证明:如下图所示,选择互相垂直的两条对角线所在的直线为坐标轴.本题关键是求出圆心O′的坐标.过O′作AC的垂线,垂足为M,M是AC的中点,垂足M的横坐标与O′的横坐标一致.同理可求出O′的纵坐标.
 如上图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
如上图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
过四边形ABCD外接圆的圆心O′分别作AC、BD、AD的垂线,垂足分别为M、N、E,则M、N、E分别是线段AC、BD、AD的中点,由线段的中点坐标公式,得
x =xM=
=xM=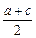 ,y
,y =yN=
=yN= ,xE=
,xE= ,yE=
,yE= .
.
所以|O′E|= =
=
 .
.
又|BC|= ,
,
所以|O′E|= |BC|.
|BC|.
 如上图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).
如上图所示,以四边形ABCD互相垂直的对角线CA、DB所在直线分别为x轴、y轴,建立直角坐标系.设A(a,0),B(0,b),C(c,0),D(0,d).过四边形ABCD外接圆的圆心O′分别作AC、BD、AD的垂线,垂足分别为M、N、E,则M、N、E分别是线段AC、BD、AD的中点,由线段的中点坐标公式,得
x
 =xM=
=xM=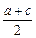 ,y
,y =yN=
=yN= ,xE=
,xE= ,yE=
,yE= .
.所以|O′E|=
 =
=
 .
.又|BC|=
 ,
,所以|O′E|=
 |BC|.
|BC|.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
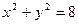 内有一点
内有一点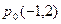 ,AB为过点
,AB为过点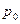 且倾斜角为α的弦,
且倾斜角为α的弦,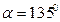 时,求AB的长;
时,求AB的长;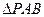 所在的平面
所在的平面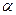 和四边形
和四边形 所在的平面
所在的平面 垂直,且
垂直,且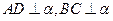 ,
,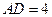 ,
,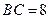 ,
,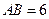 ,
,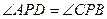 ,则点
,则点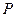 在平面
在平面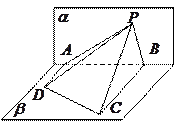
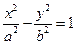 的离心率
的离心率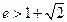 ,左、右焦点分别为
,左、右焦点分别为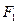 ,
,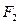 ,左准线为
,左准线为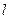 ,能否在双曲线的左支上找到一点
,能否在双曲线的左支上找到一点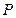 ,使得
,使得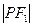 是
是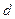 与
与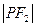 的等比中项?
的等比中项?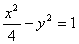 , 直线
, 直线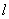 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
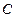 :
: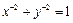 的下列说法:①关于原点对称;②关于直线
的下列说法:①关于原点对称;②关于直线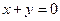 对称;③是封闭图形,面积大于
对称;③是封闭图形,面积大于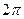 ;④不是封闭图形,与圆
;④不是封闭图形,与圆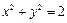 无公共点;⑤与曲线D:
无公共点;⑤与曲线D: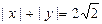 的四个交点恰为正方形的四个顶点,其中正确的序号是 .
的四个交点恰为正方形的四个顶点,其中正确的序号是 .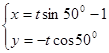 (t为参数),则直线的倾斜角为( )
(t为参数),则直线的倾斜角为( )  是两条不同的直线,
是两条不同的直线, 是一个平面,有下列四个命题:
是一个平面,有下列四个命题:  ,则
,则 ; ② 若
; ② 若 ,则
,则 ,则
,则 ;④ 若
;④ 若 ,则
,则 .
.