Question

（本题满分16分）

已知椭圆的左顶点和右焦点分别为，右准线为直线，圆D：．

（1）若点在圆D上，且椭圆的离心率为，求椭圆C的方程；

（2）若直线上存在点Q，使为等腰三角形，求椭圆C的离心率的取值范围；

（3）若点在（1）中的椭圆C上，且过点P可作圆D的两条切线，切点分别为M、N，求弦长MN的取值范围．

Answer 1

解(1)对,令,则.

所以,, ……………………………………2分

又因为,,所以,, ……………………3分

……………………………………4分

所以,椭圆的方程为:. ……………………5分

(2)由图知为等腰三角形

………………………………7分

所以,,

,

又,所以,即椭圆离心率取值范围为.……10分

(3)连交于,连,则由圆的几何性质知:为的中点,,.

所以,

⊙:，

所以,              …………………………………13分

设,则且

所以,

所以,                  ……………………………………15分

所以,. …………………………………16分

另解：设,则且

圆D:,所以直线的方程:

即：              …………………………………12分

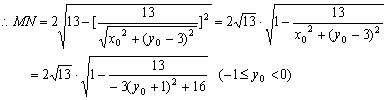…………………15分

                        …………………………………16分