题目内容
4.抛物线y=x2上的点到直线y=2x-6的最短距离为$\sqrt{5}$.分析 设P(x,x2)为抛物线上的任意一点,利用点到直线的距离公式可得:点P到直线y=2x-6的距离d=$\frac{|2x-{x}^{2}-6|}{\sqrt{5}}$=$\frac{|(x-1)^{2}+5|}{\sqrt{5}}$,再利用二次函数的单调性即可得出.
解答 解:设P(x,x2)为抛物线上的任意一点,
则点P到直线y=2x-6的距离d=$\frac{|2x-{x}^{2}-6|}{\sqrt{5}}$=$\frac{|(x-1)^{2}+5|}{\sqrt{5}}$$≥\frac{5}{\sqrt{5}}$=$\sqrt{5}$,当x=1时取等号,即取P(1,1).
故答案为:$\sqrt{5}$.
点评 本题考查了抛物线的标准方程及其性质、点到直线的距离公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
 已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.
已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点. 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )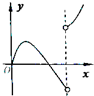



 已知△AOB是以原点O为直角顶点的抛物线x2=2py(p>0)的内接直角三角形(如图),求△AOB面积的最小值.
已知△AOB是以原点O为直角顶点的抛物线x2=2py(p>0)的内接直角三角形(如图),求△AOB面积的最小值.