题目内容
5.是否存在常数a,b使等式$\frac{1}{1•3}$+$\frac{1}{3•5}$+…$\frac{1}{(2n-1)(2n+1)}$=$\frac{n}{an+b}$对一切正整数n都成立?如存在,求出a,b的值;如不存在,请说明理由.分析 利用裂项法进行求解,解方程组即可得到结论.
解答 解:∵$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{4}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴$\frac{1}{1•3}$+$\frac{1}{3•5}$+…$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{4}$(1-$\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+$$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{4}$(1-$\frac{1}{2n+1}$)=$\frac{n}{4n+2}$,
若等式$\frac{1}{1•3}$+$\frac{1}{3•5}$+…$\frac{1}{(2n-1)(2n+1)}$=$\frac{n}{an+b}$对一切正整数n都成立,
则$\frac{n}{4n+2}$=$\frac{n}{an+b}$对一切正整数n都成立,
即a=4,b=2,
故存在常数a=4,b=2使等式$\frac{1}{1•3}$+$\frac{1}{3•5}$+…$\frac{1}{(2n-1)(2n+1)}$=$\frac{n}{an+b}$对一切正整数n都成立.
点评 本题主要考查数列求和的应用,利用裂项法是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知集合A={x|y=$\sqrt{{x}^{2}-2x-3}$},B={y|y=3sinx-1},则集合B∩∁RA=( )
| A. | (-1,2] | B. | ∅ | C. | [-4,-1] | D. | [-4,3) |
 已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.
已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.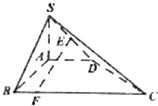 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.