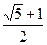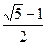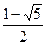题目内容
(本小题16分)
已知数列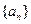 满足:
满足: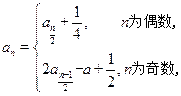 (
(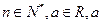 为常数),数列
为常数),数列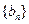 中,
中,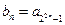 。
。
(1)求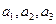 ;
;
(2)证明:数列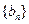 为等差数列;
为等差数列;
(3)求证:数列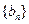 中存在三项构成等比数列时,
中存在三项构成等比数列时,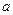 为有理数。
为有理数。
已知数列
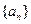 满足:
满足: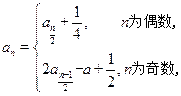 (
(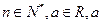 为常数),数列
为常数),数列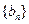 中,
中,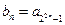 。
。(1)求
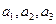 ;
;(2)证明:数列
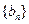 为等差数列;
为等差数列;(3)求证:数列
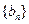 中存在三项构成等比数列时,
中存在三项构成等比数列时,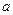 为有理数。
为有理数。(1)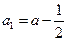 ;
;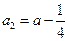 ;
;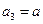
(2)证明见解析
(3)证明见解析
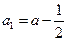 ;
;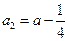 ;
;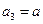
(2)证明见解析
(3)证明见解析
(1)由已知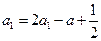 ,得
,得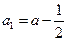 ,
,
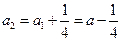 ,
,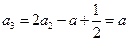 。 ……………………4分
。 ……………………4分
(2)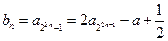 ,
,
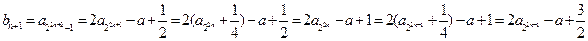
∴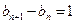 ,又
,又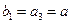 ,
,
∴数列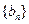 是首项为
是首项为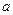 ,公差为
,公差为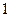 的等差数列。……………………9分
的等差数列。……………………9分
(3)证明:由⑵知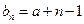 , ……………………10分
, ……………………10分
若三个不同的项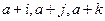 成等比数列,
成等比数列,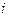 、
、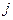 、
、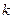 为非负整数,且
为非负整数,且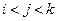 ,则
,则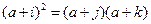 ,得
,得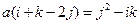 , ……………………12分
, ……………………12分
若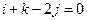 ,则
,则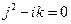 ,得
,得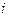 =
=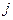 =
=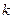 ,这与
,这与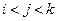 矛盾。 …………………14分
矛盾。 …………………14分
若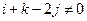 ,则
,则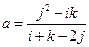 ,∵
,∵ 、
、 、
、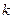 为非负整数,∴
为非负整数,∴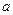 是有理数。………16分
是有理数。………16分
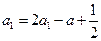 ,得
,得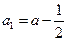 ,
,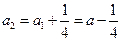 ,
,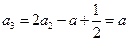 。 ……………………4分
。 ……………………4分(2)
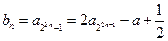 ,
,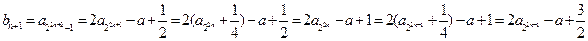
∴
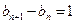 ,又
,又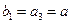 ,
,∴数列
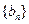 是首项为
是首项为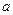 ,公差为
,公差为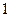 的等差数列。……………………9分
的等差数列。……………………9分(3)证明:由⑵知
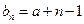 , ……………………10分
, ……………………10分若三个不同的项
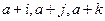 成等比数列,
成等比数列,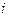 、
、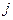 、
、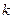 为非负整数,且
为非负整数,且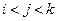 ,则
,则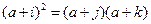 ,得
,得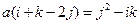 , ……………………12分
, ……………………12分若
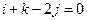 ,则
,则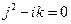 ,得
,得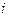 =
=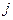 =
=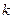 ,这与
,这与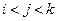 矛盾。 …………………14分
矛盾。 …………………14分若
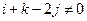 ,则
,则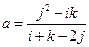 ,∵
,∵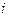 、
、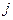 、
、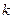 为非负整数,∴
为非负整数,∴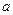 是有理数。………16分
是有理数。………16分
练习册系列答案
相关题目
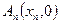 满足:
满足: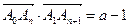 (其中
(其中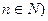 ,又知
,又知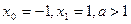 .
. 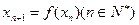 ,求
,求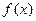 的表达式;
的表达式; 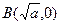 记
记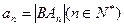 ,且
,且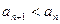 对一切
对一切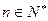 恒成立,试求
恒成立,试求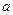 的取值范围;
的取值范围;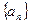 的前
的前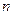 项和为
项和为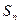 ,试证:
,试证: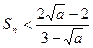 .
.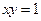 ,过
,过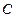 上一点
上一点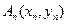 作一斜率为
作一斜率为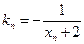 的直线交曲线C于另一点
的直线交曲线C于另一点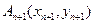 ,点
,点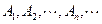 的横坐标构成数列
的横坐标构成数列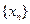 ,其中
,其中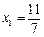 .
.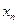 与
与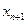 的关系式;
的关系式;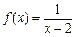 ,
,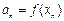 ,求
,求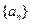 的通项公式;
的通项公式;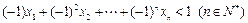 .
.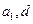 为实数,首项为
为实数,首项为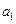 ,公差为
,公差为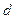 的等差数列
的等差数列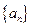 的前
的前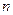 项和为
项和为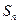 ,满足
,满足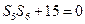 ,
,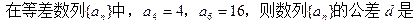 ( )
( )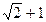 与
与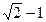 两数的等差中项是
两数的等差中项是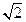
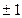
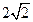
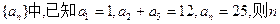 为 ( )
为 ( )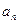 }的公比q≠1,且
}的公比q≠1,且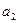 ,
,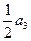 ,
,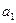 成等差数列,则
成等差数列,则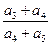 的值为( )
的值为( )