题目内容
【题目】已知函数
（1）当
时，求不等式
的解集；
（2）若
，且对任意
，
恒成立，求
的最小值．
【答案】（1）
；（2）1．
【解析】
(1) 当
时，求出分段函数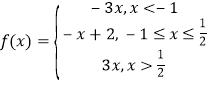
，然后可以选择数形结合求解或选择解不等式组；
(2)当
时，化简分段函数得
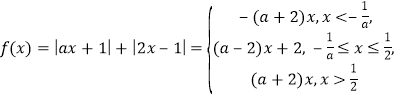
可以得到函数
在
上单调递减，在
上单调递减，在
上单调递增，然后利用最值分析法，即可求出参数
的最小值.
（1）当时，
，即，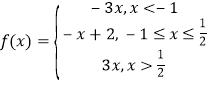
解法一：作函数的图象，它与直线
的交点为
，
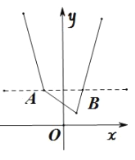
所以，
的解集的解集为
．
解法2：原不等式等价于
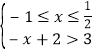或
或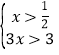
，
解得：
或无解或
，
所以，的解集为．
（2）
．
则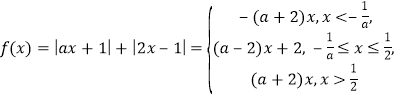
所以函数在上单调递减，在上单调递减，在上单调递增．
所以当
时，取得最小值，
．
因为对
，
恒成立，
所以
．
又因为
，
所以
，
解得
（
不合题意）．
所以的最小值为1．
【题目】红星海水养殖场进行某水产品的新旧养殖方法的产量对比，收货时在旧养殖的大量网箱中随机抽取
个网箱，在新养殖法养殖的大量网箱中也随机抽取个网箱，测量各箱水产品的产量，得样本频率分布直方图如下：
（1）填写下列列联表，并根据列联表判断是否有
的把握认为箱产量与养殖方法有关.
养殖法 箱产量 | 箱产量 | 箱产量 | 总计 |
旧养殖法 | |||
新养殖法 | |||
总计 |
（2）设两种养殖方法的产量互相独立，记
表示事件：“旧养殖法的箱产量低于
，新养殖法的箱产量不低于 ”，估计的概率；
（3）某水产批发户从红星海水养殖场用新养殖法养殖的大量网箱水产品中购买了
个网箱的水产品，记
表示箱产量位于区间
的网箱个数，以上样本在相应区间的频率代替概率，求
.
|
|
|
|
|
|
|
|
|
|
|
|
（
，其中
）
【题目】共享单车的投放，方便了市民短途出行，被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度，随机调查了100位成人市民，统计数据如下：
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
（1）求出列联表中字母x、y、m、n的值；
（2）①从此样本中，对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研，其中不小于40岁的人应抽多少人？
②从独立性检验角度分析，能否有
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考：
P（ | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理， 
得到下表2：
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z关于t的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程
，其中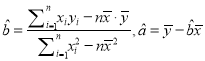
）
