题目内容

直线l：cosθ•x+sinθ•y=1（θ∈R）与圆C：x2+y2=1的位置关系是（　　）
分析：利用点到直线的距离公式求出圆心到已知直线的距离d，比较d与r的大小即可得到直线与圆的位置关系．
解答：解：由题设知圆心（0，0）到直线的距离
d=
|-1|
cos2θ+sin2θ
=1，
∵圆的半径r=1，∴d=r
∴直线xcosθ+ysinθ-2=0与圆x2+y2=1相切
故选B．
点评：本题考查直线与圆的位置关系，以及平方关系的应用，求得圆心到已知直线的距离d，比较d与r的大小是关键．
练习册系列答案
相关题目
本题有（I）、（II）、（III）三个选作题，每题7分，请考生任选两题作答，满分14分．如果多做，则按所做的前两题记分，作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
已知a∈R，矩阵P=
02
-10
，Q=
01
a0
，若矩阵PQ对应的变换把直线l1：x-y+4=0变为直线l2：x+y+4=0，求实数a的值．
（2）选修4-4：坐标系与参数方程
在极坐标系中，求圆C：ρ=2上的点P到直线l：ρ(cosθ+
3
sinθ)=6的距离的最小值．
（3）选修4-5：不等式选讲
已知实数x，y满足x2+4y2=a（a＞0），且x+y的最大值为5，求实数a的值．
（选修4-4：坐标系与参数方程）将曲线C1：
x=
2
t2+1
y=
2t
t2+1
，化为普通方程，并求C1被直线l：ρcos(θ+
π
3
)=1所截得的线段长．
（2013•怀化三模）直线l：ρcosθ=t（常数t＞0）与圆
x=cosθ
y=1+sinθ
（θ为参数）相切，则t=
±1
±1
．
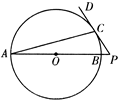精英家教网（1）如图，AB是圆O的直径，P在AB的延长线上，PD切圆O于点C．已知圆O半径为y=x-1（1≤x≤2），OP=2，则PC=
 
，∠ACD的大小为
 
．
（2）在极坐标系中，点（2，
π2
）关于直线l：ρcosθ=1的对称点的一个极坐标为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网