ћвƒњƒЏ»Ё
±Њћв”–£®I£©°Ґ£®II£©°Ґ£®III£©»эЄц—°„чћв£ђ√њћв7Ј÷£ђ«лњЉ…ъ»ќ—°Ѕљћв„чір£ђ¬ъЈ÷14Ј÷£Ѓ»зєыґа„ц£ђ‘т∞іЋщ„цµƒ«∞ЅљћвЉ«Ј÷£ђ„чір ±£ђѕ»”√2B«¶± ‘Џірћвњ®…ѕ∞—Ћщ—°ћвƒњґ‘”¶µƒћвЇ≈ЌњЇЏ£ђ≤ҐљЂЋщ—°ћвЇ≈ћо»лј®Ї≈÷–£Ѓ
£®1£©—°–ё4-2£ЇЊЎ’у”л±дїї
“—÷™a° R£ђЊЎ’уP=
£ђQ=
£ђ»фЊЎ’уPQґ‘”¶µƒ±дїї∞—÷±ѕяl1£Їx-y+4=0±дќ™÷±ѕяl2£Їx+y+4=0£ђ«у µ эaµƒ÷µ£Ѓ
£®2£©—°–ё4-4£Ї„ш±кѕµ”л≤ќ эЈљ≥ћ
‘ЏЉЂ„ш±кѕµ÷–£ђ«у‘≤C£Ї¶—=2…ѕµƒµгPµљ÷±ѕяl£Ї¶—(cos¶»+
sin¶»)=6µƒЊајлµƒ„о–°÷µ£Ѓ
£®3£©—°–ё4-5£Ї≤їµ» љ—°љ≤
“—÷™ µ эx£ђy¬ъ„гx2+4y2=a£®a£Њ0£©£ђ«“x+yµƒ„оіу÷µќ™5£ђ«у µ эaµƒ÷µ£Ѓ
£®1£©—°–ё4-2£ЇЊЎ’у”л±дїї
“—÷™a° R£ђЊЎ’уP=
|
|
£®2£©—°–ё4-4£Ї„ш±кѕµ”л≤ќ эЈљ≥ћ
‘ЏЉЂ„ш±кѕµ÷–£ђ«у‘≤C£Ї¶—=2…ѕµƒµгPµљ÷±ѕяl£Ї¶—(cos¶»+
| 3 |
£®3£©—°–ё4-5£Ї≤їµ» љ—°љ≤
“—÷™ µ эx£ђy¬ъ„гx2+4y2=a£®a£Њ0£©£ђ«“x+yµƒ„оіу÷µќ™5£ђ«у µ эaµƒ÷µ£Ѓ
Ј÷ќц£Ї£®1£©ѕ»Љ∆ЋгЊЎ’уABґ‘”¶µƒ±дїї£ђ‘ў«у≥ц‘Џ±дїїѕ¬µгµƒ„ш±к÷ЃЉдµƒґ‘”¶єЎѕµ£ђі”ґшњ…«у÷±ѕяl2µƒЈљ≥ћ£ђ„оЇу”л“—÷™Јљ≥ћґ‘’’њ…µ√µљa÷µ£Ѓ
£®2£©‘≤p=2°Ґ÷±ѕяp£®cos¶»+
sin¶»£©=6їѓќ™÷±љ«„ш±кЈљ≥ћ£ђ«у≥ц‘≤–ƒµљ÷±ѕяµƒЊајл£ђ‘ў«у‘≤p=2…ѕµƒµгµљ÷±ѕяp£®cos¶»+
sin¶»£©=6µƒЊајлµƒ„о–°÷µ£Ѓ
£®3£©њ……и≥цЌ÷‘≤x2+4y2=a≤ќ эЈљ≥ћ£ђ„™їѓќ™»эљ«Їѓ э£ђјы”√»эљ«Їѓ эµƒ”–љз–‘«у„о÷µ£ђі”ґшµ√≥цaµƒ÷µ£Ѓ
£®2£©‘≤p=2°Ґ÷±ѕяp£®cos¶»+
| 3 |
| 3 |
£®3£©њ……и≥цЌ÷‘≤x2+4y2=a≤ќ эЈљ≥ћ£ђ„™їѓќ™»эљ«Їѓ э£ђјы”√»эљ«Їѓ эµƒ”–љз–‘«у„о÷µ£ђі”ґшµ√≥цaµƒ÷µ£Ѓ
љвір£Їљв£Ї£®1£©°яЊЎ’уP=
£ђQ=
£ђ
°аPQ=
°≠£®3Ј÷£©£ђ
‘Џ÷±ѕяl1…ѕ»ќ»°“їµгP£®x£ђy£©£ђЊ≠ЊЎ’уPQ±дїїќ™µгQ£®x°д£ђy°д£©£ђ‘т
£®x£ђy£©
=£®x°д£ђy°д£©£ђ
Љі
°≠£®8Ј÷£©
іъ»лx+y+4=0÷–µ√2ax-y+4=0£ђ
°а2a=1£ђa=
£ї
£®2£©‘≤p=2°Ґ÷±ѕяp£®cos¶»+
sin¶»£©=6їѓќ™÷±љ«„ш±кЈљ≥ћ£ђ
Ј÷±рќ™x2+y2=4£ђx+
y-6=0
‘≤–ƒµљ÷±ѕяµƒЊајлќ™£Ї
=3
Ћщ“‘‘≤p=2…ѕµƒµгµљ÷±ѕяp£®cos¶»+
sin¶»£©=6µƒЊајлµƒ„о–°÷µ «3-2=1
£®3£©x2+4y2=a≤ќ эЈљ≥ћ «
£ђ¶»° R
‘тx+y=
cos¶»+
sin¶»=
sin(¶»+∅)£ђ
°аx+yµƒ„оіу÷µќ™
=5£ђљвµ√a=20£Ѓ
|
|
°аPQ=
|
‘Џ÷±ѕяl1…ѕ»ќ»°“їµгP£®x£ђy£©£ђЊ≠ЊЎ’уPQ±дїїќ™µгQ£®x°д£ђy°д£©£ђ‘т
£®x£ђy£©
|
Љі
|
іъ»лx+y+4=0÷–µ√2ax-y+4=0£ђ
°а2a=1£ђa=
| 1 |
| 2 |
£®2£©‘≤p=2°Ґ÷±ѕяp£®cos¶»+
| 3 |
Ј÷±рќ™x2+y2=4£ђx+
| 3 |
‘≤–ƒµљ÷±ѕяµƒЊајлќ™£Ї
| |-6| | ||
|
Ћщ“‘‘≤p=2…ѕµƒµгµљ÷±ѕяp£®cos¶»+
| 3 |
£®3£©x2+4y2=a≤ќ эЈљ≥ћ «
|
‘тx+y=
| a |
| ||
| 2 |
|
°аx+yµƒ„оіу÷µќ™
|
µг∆ј£ЇњЉ≤йЊЎ’у±дїї£ђњЉ≤йЊЎ’у±дїїµƒ‘Ћ”√£ђµгµљ÷±ѕяµƒЊајлєЂ љ£ђЉтµ•«ъѕяµƒЉЂ„ш±кЈљ≥ћЇЌ÷±љ«„ш±кЈљ≥ћµƒї•їѓ£ђњЉ≤йЉ∆Ћгƒ№Ѕ¶£ђ «їщі°ћв£Ѓ

ЅЈѕ∞≤бѕµЅ–ір∞Є
 »Ђ”≈≥еіћ100Ј÷ѕµЅ–ір∞Є
»Ђ”≈≥еіћ100Ј÷ѕµЅ–ір∞Є ”Ґ≤≈µгљтѕµЅ–ір∞Є
”Ґ≤≈µгљтѕµЅ–ір∞Є
ѕаєЎћвƒњ
 ±Њћв”–£®1£©£ђ£®2£©£ђ£®3£©»эЄц—°ірћв£ђ√њћв7Ј÷£ђ«лњЉ…ъ»ќ—°2ћв„чір£ђ¬ъЈ÷14Ј÷£Ѓ»зєыґа„ц£ђ‘т∞іЋщ„цµƒ«∞ЅљћвЉ∆Ј÷£Ѓ„чір ±£ђѕ»”√2B«¶± ‘Џірћвњ®…ѕ∞—Ћщ—°ћвƒњґ‘”¶µƒћвЇ≈ЌњЇЏ£Ѓ
±Њћв”–£®1£©£ђ£®2£©£ђ£®3£©»эЄц—°ірћв£ђ√њћв7Ј÷£ђ«лњЉ…ъ»ќ—°2ћв„чір£ђ¬ъЈ÷14Ј÷£Ѓ»зєыґа„ц£ђ‘т∞іЋщ„цµƒ«∞ЅљћвЉ∆Ј÷£Ѓ„чір ±£ђѕ»”√2B«¶± ‘Џірћвњ®…ѕ∞—Ћщ—°ћвƒњґ‘”¶µƒћвЇ≈ЌњЇЏ£Ѓ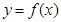 ¬ъ„г
¬ъ„г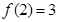 £ђ«“ґ‘»ќ“в
£ђ«“ґ‘»ќ“в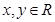 ґЉ”–
ґЉ”–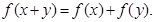
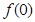 µƒ÷µ≤Ґ÷§√чЇѓ э
µƒ÷µ≤Ґ÷§√чЇѓ э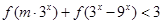 ґ‘»ќ“в
ґ‘»ќ“в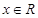 Їг≥…ЅҐ£ђ«у µ эmµƒ»°÷µЈґќІ°£
Їг≥…ЅҐ£ђ«у µ эmµƒ»°÷µЈґќІ°£