题目内容
设F1,F2分别是椭圆C: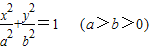 的左右焦点,
的左右焦点,(1)设椭圆C上的点
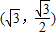 到F1,F2两点距离之和等于4,写出椭圆C的方程和焦点坐标
到F1,F2两点距离之和等于4,写出椭圆C的方程和焦点坐标(2)设K是(1)中所得椭圆上的动点,求线段KF1的中点B的轨迹方程
(3)设点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM,PN的斜率都存在,并记为kPM,KPN试探究kPM•KPN的值是否与点P及直线L有关,并证明你的结论.
【答案】分析:(1)根据椭圆C上的点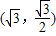 到F1,F2两点距离之和等于4,可知2a=4,求得a.把点
到F1,F2两点距离之和等于4,可知2a=4,求得a.把点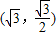 和a代入椭圆的标准方程,可求得b.进而可得椭圆的标准方程和焦点坐标.
和a代入椭圆的标准方程,可求得b.进而可得椭圆的标准方程和焦点坐标.
(2)设KF1的中点为B(x,y)则点K(2x+1,2y),把K的坐标代入椭圆的标准方程,可得到x和y的关系式即点B的轨迹方程
(3)设M(x,y),N(-x,-y),p(x,y) 把这些点代入椭圆的标准方程,得到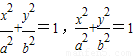 后两式相减可得到
后两式相减可得到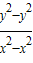 的值,然后表示出kPM,KPN后相乘并将
的值,然后表示出kPM,KPN后相乘并将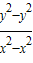 的值代入可得到结论.
的值代入可得到结论.
解答:解:(1)由于点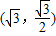 在椭圆上,
在椭圆上,
2a=4,
椭圆C的方程为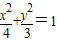
焦点坐标分别为(-1,0),(1,0)
(2)设KF1的中点为B(x,y)则点K(2x+1,2y)
把K的坐标代入椭圆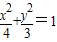 中得
中得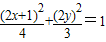
线段KF1的中点B的轨迹方程为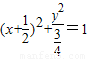
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设M(x,y)N(-x,-y),p(x,y)
M,N,P在椭圆上,应满足椭圆方程,
得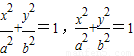
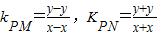
kPM•KPN=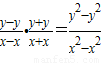 =-
=-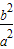
kPM•KPN的值与点P及直线L无关
点评:本题主要考查椭圆的标准方程和直线与椭圆的综合问题.椭圆在圆锥曲线中所占比重最大,考查的也最多,要强化复习.
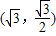 到F1,F2两点距离之和等于4,可知2a=4,求得a.把点
到F1,F2两点距离之和等于4,可知2a=4,求得a.把点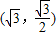 和a代入椭圆的标准方程,可求得b.进而可得椭圆的标准方程和焦点坐标.
和a代入椭圆的标准方程,可求得b.进而可得椭圆的标准方程和焦点坐标.(2)设KF1的中点为B(x,y)则点K(2x+1,2y),把K的坐标代入椭圆的标准方程,可得到x和y的关系式即点B的轨迹方程
(3)设M(x,y),N(-x,-y),p(x,y) 把这些点代入椭圆的标准方程,得到
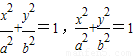 后两式相减可得到
后两式相减可得到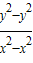 的值,然后表示出kPM,KPN后相乘并将
的值,然后表示出kPM,KPN后相乘并将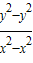 的值代入可得到结论.
的值代入可得到结论.解答:解:(1)由于点
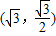 在椭圆上,
在椭圆上,
2a=4,
椭圆C的方程为
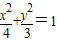
焦点坐标分别为(-1,0),(1,0)
(2)设KF1的中点为B(x,y)则点K(2x+1,2y)
把K的坐标代入椭圆
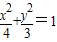 中得
中得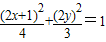
线段KF1的中点B的轨迹方程为
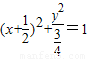
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设M(x,y)N(-x,-y),p(x,y)
M,N,P在椭圆上,应满足椭圆方程,
得
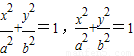
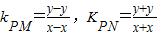
kPM•KPN=
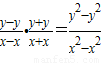 =-
=-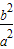
kPM•KPN的值与点P及直线L无关
点评:本题主要考查椭圆的标准方程和直线与椭圆的综合问题.椭圆在圆锥曲线中所占比重最大,考查的也最多,要强化复习.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
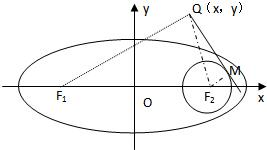 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: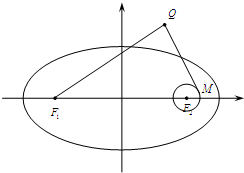 设F1、F2分别是椭圆
设F1、F2分别是椭圆