题目内容
8.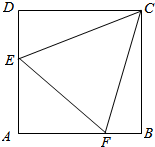 在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的
在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的周长为2;(Ⅰ)设∠BCF=α,∠ECD=β,$AE=AF=2-\sqrt{2}$,求tanα,tanβ.
(Ⅱ)求∠ECF的度数.
分析 (Ⅰ)根据AE、AF的值求出DE和BF,在RT△CBF和RT△CDE中求出tanα,tanβ;
(Ⅱ)利用两角和的正切函数求出tan(α+β)的值,由α、β的范围求出α+β的值,再求出∠ECF的度数.
解答 解:(Ⅰ)∵$AE=AF=2-\sqrt{2}$,∴DE=BF=$\sqrt{2}-1$,
在RT△CBF中,tanα=$\frac{BF}{BC}$=$\sqrt{2}-1$,
在RT△CDE中,tanβ=$\frac{DE}{DC}$=$\sqrt{2}-1$;
(Ⅱ)由(Ⅰ)得,tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$
=$\frac{2(\sqrt{2}-1)}{1-(\sqrt{2}-1)^{2}}$=$\frac{2(\sqrt{2}-1)}{1-(3-2\sqrt{2})}$=1,
∵α+β∈(0,$\frac{π}{2}$),∴α+β=$\frac{π}{4}$,
则∠ECF=$\frac{π}{2}$-(α+β)=$\frac{π}{4}$.
点评 本题考查两角和的正切函数,以及正切函数的定义,注意角的范围和正切函数的符号,属于中档题.

练习册系列答案
相关题目
3.等差数列{an}中,首项a1=1,a5=9,则数列的前10项之和是( )
| A. | 90 | B. | 100 | C. | 145 | D. | 190 |
17.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(sinα,cosα),且$\overrightarrow{a}∥\overrightarrow{b}$,则tanα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |