题目内容
【题目】已知函数![]() 在点(1,f(1))处的切线为y=1.
在点(1,f(1))处的切线为y=1.
(1)求a,b的值;
(2)问是否存在实数m,使得当x∈(0,1]时,![]() 的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
的最小值为0?若存在求出m的取值范围;若不存在,请说明理由.
【答案】(1)a=1,b=2. (2)(-∞,2].
【解析】
试题分析:(1)求函数的导数,利用导数的几何意义,建立方程关系即可求实数a,b的值;(2)求函数的导数,利用函数的最小值,建立条件关系即可得到结论
试题解析:(1)因为![]() ,其定义域为(0,+∞),所以
,其定义域为(0,+∞),所以![]()
依题意可得![]() 解得a=1,b=2.
解得a=1,b=2.
(2)![]() ,
,
所以![]()
①当m≤0时,![]() ,则g(x)在(0,1]上单调递减,所以
,则g(x)在(0,1]上单调递减,所以![]()
②当0<m≤2时,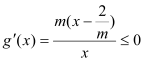 ,则g(x)在(0,1]上单调递减,
,则g(x)在(0,1]上单调递减,
所以![]()
③当m>2时,则![]() 时,
时,![]() 时,
时,![]()
所以g(x)在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,1]上单调递增,
,1]上单调递增,
故当![]() 时,g(x)取最小值为g(
时,g(x)取最小值为g(![]() ).
).
因为g(![]() )<g(1)=0,所以
)<g(1)=0,所以![]()
综上所述,存在m满足题意,其取值范围为(-∞,2].

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目

