Question

（本小题满分14分）

已知定点A（1，0）和定直线x＝－1的两个动点E、F，满足AE⊥AF，动点P满足EP∥OA，FO∥OP（其中O为坐标原点）.

（1）求动点P的轨迹C的方程；

（2）过点B（0，2）的直线l与（1）中轨迹C相交于两个不同的点M、N，若∠MAN为钝角，求直线l的斜率的取值范围；

（3）过点T（－1，0）作直线m与（1）中的轨迹C交于两点G、H，问在x轴上是否存在一点D，使△DGH为等边三角形；若存在，试求出点D的坐标；若不存在，请说明理由.

Answer 1

解：

（1）设P（x，y），E（－1，y₁），F（－1，y₂）（y₁、y₂均不为0），

由EP∥OA得y₁＝y，即E（－1，y）.

由FO∥OP得y₂＝－，即F（―1，―），得

AE·AF＝0   （2，－y₁）·（2，y₂）＝0

  y₁y₂＝－4

  y²＝4x（x≠0）

所以动点P的轨迹C的方程为y²＝4x（x≠0）.

（3分）

（2）设直线l的方程y＝kx＋2（k≠0），M（，y₁），N（，y₂）联立得消去x得ky²－4y＋8＝0，所以y₁＋y₂＝，y₁y­₂＝，且△＝16－32k＞0，即k＜.

所以AM·AN＝·

＝ ＋y₁y­₂

＝

＝＋

因为∠MAN为钝角，所以AM·AN＜0，所以－12＜k＜0.

（8分）

（3）设m：y＝k(x＋1)（k≠0），代入y²＝4x，得k²x²＋2(k²－2)x＋k²＝0，

由，△＝[2(k²―2)]²―4k²·k²＝－16k²＋16＞0，得|k|＜1.

设G（x₁，y₁），H（x₂，y₂），则x₁＋x₂＝，x₁x₂＝1，

所以|GH|＝·＝·

＝.

GH的中点Q的坐标为（，）.

假设存在点D（x₀，0），使△DGH为等边三角形，又边GH的中垂线方程为

y－＝―(x―).

由D在此中垂线上，得0－＝―(x₀―)，x₀＝＋1.

（11分）

设d为D到直线l的距离，由正三角形的条件有|GH|＝d，可得

，

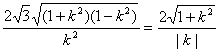即3(1－k²)＝k²，k²＝，所以k＝±，x₀＝，故存在点D（，0），使△DGH为等边三角形.