题目内容
(本小题满分16分)
已知函数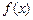 =
=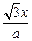 +
+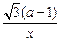 ,a≠0且a≠1.
,a≠0且a≠1.
(1)试就实数a的不同取值,写出该函数的单调增区间;
(2)已知当x>0时,函数在(0,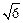 )上单调递减,在(
)上单调递减,在(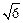 ,
,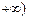 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;
(3)记(2)中的函数图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出直线l的方程;若不存在,请说明理由.
已知函数
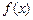 =
=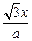 +
+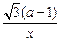 ,a≠0且a≠1.
,a≠0且a≠1.(1)试就实数a的不同取值,写出该函数的单调增区间;
(2)已知当x>0时,函数在(0,
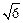 )上单调递减,在(
)上单调递减,在(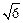 ,
,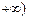 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;(3)记(2)中的函数图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出直线l的方程;若不存在,请说明理由.
解析:(1)①当a<0时,函数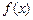 的单调增区间为(
的单调增区间为(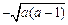 ,0),(0,
,0),(0,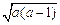 );
);
②当0<a<1时,函数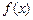 的单调增区间为
的单调增区间为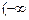 ,0),(0,
,0),(0,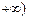 ;
;
③当a>1时,函数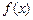 的单调增区间为
的单调增区间为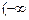 ,
,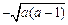 ),(
),(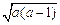 ,
,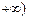 .
.
(2)由题设及(1)中③知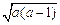 =
=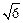 ,且a>1,解得a=3,因此函数解析式为
,且a>1,解得a=3,因此函数解析式为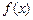 =
=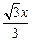 +
+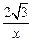 ( x≠0).
( x≠0).
(3)假设存在经过原点的直线l为曲线C的对称轴,显然x,y轴不是曲线C的对称轴,故可设l:y=kx(k≠0).
设P(p,q)为曲线C上的任意一点, 与P(p,q)关于直线l对称,且p≠
与P(p,q)关于直线l对称,且p≠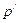 ,q≠
,q≠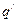 ,则
,则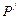 也在曲线C上,由此得
也在曲线C上,由此得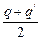 =
=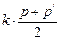 ,
,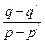 =
=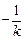 ,且q=
,且q= +
+ ,
,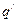 =
=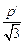 +
+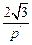 ,整理得k
,整理得k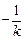 =
=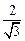 ,解得k=
,解得k=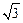 或k=
或k=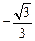 .
.
所以存在经过原点的直线y=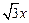 及y=
及y=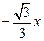 为曲线C的对称轴.
为曲线C的对称轴.
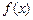 的单调增区间为(
的单调增区间为(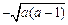 ,0),(0,
,0),(0,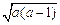 );
);②当0<a<1时,函数
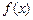 的单调增区间为
的单调增区间为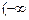 ,0),(0,
,0),(0,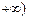 ;
;③当a>1时,函数
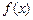 的单调增区间为
的单调增区间为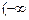 ,
,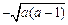 ),(
),(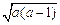 ,
,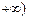 .
.(2)由题设及(1)中③知
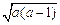 =
=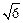 ,且a>1,解得a=3,因此函数解析式为
,且a>1,解得a=3,因此函数解析式为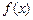 =
=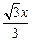 +
+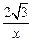 ( x≠0).
( x≠0).(3)假设存在经过原点的直线l为曲线C的对称轴,显然x,y轴不是曲线C的对称轴,故可设l:y=kx(k≠0).
设P(p,q)为曲线C上的任意一点,
 与P(p,q)关于直线l对称,且p≠
与P(p,q)关于直线l对称,且p≠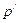 ,q≠
,q≠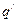 ,则
,则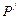 也在曲线C上,由此得
也在曲线C上,由此得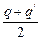 =
=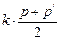 ,
,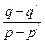 =
=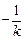 ,且q=
,且q= +
+ ,
,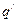 =
=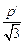 +
+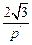 ,整理得k
,整理得k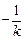 =
=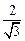 ,解得k=
,解得k=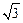 或k=
或k=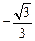 .
.所以存在经过原点的直线y=
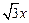 及y=
及y=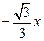 为曲线C的对称轴.
为曲线C的对称轴.略

练习册系列答案
相关题目
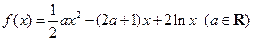 .
.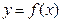 在
在 和
和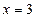 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;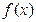 的单调区间;
的单调区间;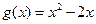 ,若对任意
,若对任意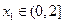 ,均存在
,均存在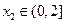 ,使得
,使得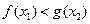 ,求
,求 (万元)与产量
(万元)与产量 (台)之间的函数关系式是
(台)之间的函数关系式是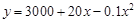
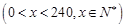 ,若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总体)的最低产量是( )
,若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总体)的最低产量是( )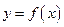 为偶函数,则函数
为偶函数,则函数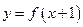 的一条对称轴是
的一条对称轴是 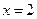
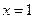
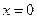


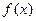 是偶
是偶 函数,且当
函数,且当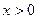 时
时 的所有
的所有 之和为 ▲
之和为 ▲  到实数集
到实数集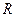 的映射过程:区间
的映射过程:区间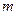 对应数轴上的点
对应数轴上的点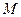 (如图
(如图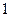 ),将线段
),将线段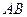 围成一个正方形,使两端点
围成一个正方形,使两端点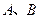 恰好重合(如图
恰好重合(如图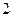 ),再将这个正方形放在平面直角坐标系中,使其中两个顶点在
),再将这个正方形放在平面直角坐标系中,使其中两个顶点在 轴上,点
轴上,点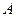 的坐标为
的坐标为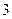 ),若图
),若图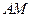 与
与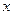 轴交于点
轴交于点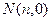 ,则
,则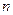 ,记作
,记作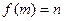 .现给出以下命题:
.现给出以下命题: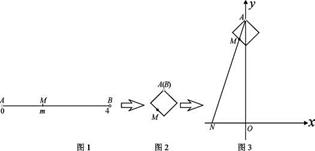
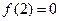 ; ②
; ②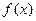 的图象关于点
的图象关于点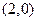 对称;
对称;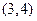 上为常数函数.
上为常数函数.