题目内容
与椭圆 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )
 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )A. | B. | C.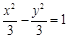 | D. |
B
试题分析:在椭圆
 中,
中,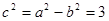 ,∴
,∴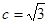 ,∴焦点为
,∴焦点为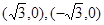 ,设所求的双曲线方程为:
,设所求的双曲线方程为: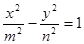
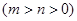 ,由双曲线的定义可知:
,由双曲线的定义可知: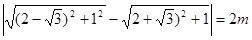 ,∴
,∴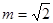 ,∴
,∴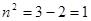 ,故双曲线方程为:
,故双曲线方程为: .
.
练习册系列答案
相关题目
题目内容
 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )A. | B. | C.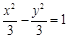 | D. |
 中,
中,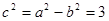 ,∴
,∴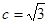 ,∴焦点为
,∴焦点为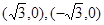 ,设所求的双曲线方程为:
,设所求的双曲线方程为: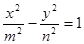
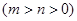 ,由双曲线的定义可知:
,由双曲线的定义可知: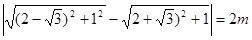 ,∴
,∴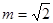 ,∴
,∴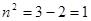 ,故双曲线方程为:
,故双曲线方程为: .
.