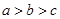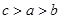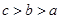题目内容
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,
f(x)=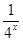 -
-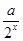 (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
f(x)=
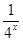 -
-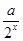 (a∈R).
(a∈R).(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
解:(1)设x∈[0,1],则-x∈[-1,0],
f(-x)=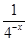 -
-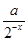 =4x-a·2x,
=4x-a·2x,
∵f(-x)=-f(x),
∴f(x)=a·2x-4x,x∈[0,1].
令t=2x,t∈[1,2],
∴g(t)=a·t-t2=-(t-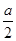 )2+
)2+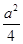 ,
,
当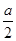 ≤1,即a≤2时,g(t)max=g(1)=a-1;
≤1,即a≤2时,g(t)max=g(1)=a-1;
当1<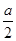 <2,即2<a<4时,g(t)max=g(
<2,即2<a<4时,g(t)max=g(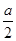 )=
)=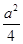 ;
;
当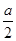 ≥2,即a≥4时,g(t)max=g(2)=2a-4.
≥2,即a≥4时,g(t)max=g(2)=2a-4.
综上,当a≤2时,f(x)的最大值为a-1;
当2<a<4时,f(x)的最大值为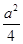 ;
;
当a≥4时,f(x)的最大值为2a-4.
(2)∵函数f(x)在[0,1]上是增函数,
∴f′(x)=aln2×2x-ln4×4x=2xln2·(a-2×2x)≥0,∴a-2×2x≥0恒成立,
∴a≥2×2x.∵2x∈[1,2],∴a≥4.
故a的取值范围是[4,+∞).
f(-x)=
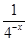 -
-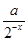 =4x-a·2x,
=4x-a·2x,∵f(-x)=-f(x),
∴f(x)=a·2x-4x,x∈[0,1].
令t=2x,t∈[1,2],
∴g(t)=a·t-t2=-(t-
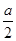 )2+
)2+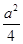 ,
,当
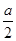 ≤1,即a≤2时,g(t)max=g(1)=a-1;
≤1,即a≤2时,g(t)max=g(1)=a-1;当1<
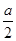 <2,即2<a<4时,g(t)max=g(
<2,即2<a<4时,g(t)max=g(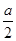 )=
)=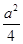 ;
;当
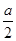 ≥2,即a≥4时,g(t)max=g(2)=2a-4.
≥2,即a≥4时,g(t)max=g(2)=2a-4.综上,当a≤2时,f(x)的最大值为a-1;
当2<a<4时,f(x)的最大值为
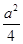 ;
;当a≥4时,f(x)的最大值为2a-4.
(2)∵函数f(x)在[0,1]上是增函数,
∴f′(x)=aln2×2x-ln4×4x=2xln2·(a-2×2x)≥0,∴a-2×2x≥0恒成立,
∴a≥2×2x.∵2x∈[1,2],∴a≥4.
故a的取值范围是[4,+∞).

练习册系列答案
相关题目
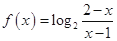 的定义域为集合
的定义域为集合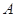 ,关于
,关于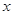 的不等式
的不等式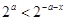 的解集为
的解集为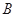 ,若
,若 ,求实数
,求实数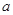 的取值范围.
的取值范围. ,
, ,
, ,
, ,则下列等式一定成立的是( )
,则下列等式一定成立的是( )



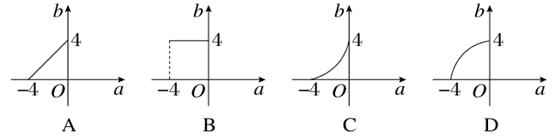
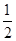 )x2+2x-1的值域是( )
)x2+2x-1的值域是( )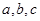 均为正数,且
均为正数,且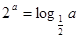 ,
,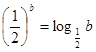 ,
,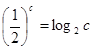 .则( )
.则( )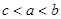
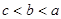
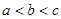
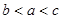
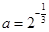 ,
,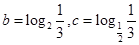 ,则( )
,则( )