题目内容
已知集合A={x|x2-5x+4≤0},B={x|x2-2ax+a+2≤0},若B⊆A,求实数a的取值范围.
A={x|x2-5x+4≤0}={x|1≤x≤4}.
设f(x)=x2-2ax+a+2,它的图象是一条开口向上的抛物线
(1)若B=ϕ,满足条件,此时△<0,即4a2-4(a+2)<0,
解得-1<a<2;
(2)若B≠ϕ,设抛物线与x轴交点的横坐标为x1,x2,
且x1≤x2,欲使B⊆A,应有{x|x1≤x≤x2}⊆{x|1≤x≤4},
结合二次函数的图象,得
即
解得2≤a≤
.
综上可知a的取值范围是(-1,
].
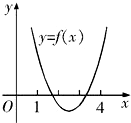
设f(x)=x2-2ax+a+2,它的图象是一条开口向上的抛物线
(1)若B=ϕ,满足条件,此时△<0,即4a2-4(a+2)<0,
解得-1<a<2;
(2)若B≠ϕ,设抛物线与x轴交点的横坐标为x1,x2,
且x1≤x2,欲使B⊆A,应有{x|x1≤x≤x2}⊆{x|1≤x≤4},
结合二次函数的图象,得
|
即
|
| 18 |
| 7 |
综上可知a的取值范围是(-1,
| 18 |
| 7 |


练习册系列答案
相关题目
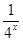 -
-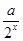 (a∈R).
(a∈R).