题目内容
已知定义域为R的函数f（x）对任意实数x、y满足f（x+y）+f（x-y）=2f（x）cosy，且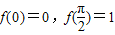
．给出下列结论：
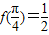；②f（x）为奇函数；③f（x）为周期函数；④f（x）在（0，x）内单调递减．其中正确的结论序号是（ ）A．②③
B．②④
C．①③
D．①④
【答案】分析：令x=y=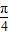
可求出f（
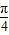）的值，得知①不对排除CD．由x=
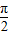可知f（x）在（0，x）内单不是调递减排除B．
解答：解：令x=y=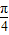
，根据f（x+y）+f（x-y）=2f（x）cosy，且
．
∴
∴
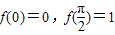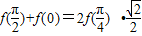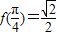故①不对
∵f（x+y）+f（x-y）=2f（x）cosy
令x=0，则
f（y）+f（-y）=f（0）cosy=0
f（-y）=-f（y）
所以f（x）是奇函数 故②对．
令x=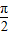
，由f（0）=0，f（
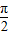）=1知④不对
故选A．
点评：本题主要考查抽象函数的有关问题．抽象函数值、单调性、周期性、奇偶性经常是考查重点．
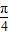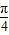可求出f（）的值，得知①不对排除CD．由x=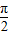可知f（x）在（0，x）内单不是调递减排除B．解答：解：令x=y=
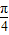，根据f（x+y）+f（x-y）=2f（x）cosy，且．∴
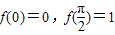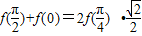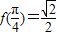∴故①不对∵f（x+y）+f（x-y）=2f（x）cosy
令x=0，则
f（y）+f（-y）=f（0）cosy=0
f（-y）=-f（y）
所以f（x）是奇函数 故②对．
令x=
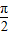，由f（0）=0，f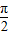（）=1知④不对故选A．
点评：本题主要考查抽象函数的有关问题．抽象函数值、单调性、周期性、奇偶性经常是考查重点．
练习册系列答案
相关题目