题目内容
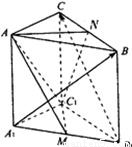
如图,在正三棱柱ABC-A1B1C1中,M,N分别为A1B1,BC之中点.(1)试求
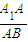 ,使
,使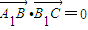 .
.(2)在(1)条件下,求二面角N-AC1-M的大小.
【答案】分析:(1)以C1点为坐标原点,C1A1所在直线为x轴,C1C所在直线为z轴,建立空间直角坐标系,设A1B1=b,AA1=a,分别求出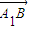 与
与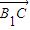 的坐标,根据
的坐标,根据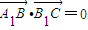 求出a与b的关系,从而求出
求出a与b的关系,从而求出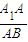 ,
,
(2)在(1)条件下,不妨设b=2,则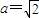 ,取AC1中点为P,根据二面角的平面角的定义可知∠NPM为二面角N-AC1-M的平面角,分别求出
,取AC1中点为P,根据二面角的平面角的定义可知∠NPM为二面角N-AC1-M的平面角,分别求出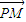 与
与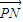 的坐标,计算它们的数量积即可求出此角.
的坐标,计算它们的数量积即可求出此角.
解答:解:(1)以C1点为坐标原点,C1A1所在直线为x轴,C1C所在直线为z轴,建立空间直角坐标系,
设A1B1=b,AA1=a(a,b∈(0,+∞).
∵三棱柱ABC-A1B1C1为正三棱柱,则A1,B,B1,C的坐标分别为:
(b,0,0),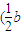 ,
,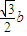 ,a),
,a),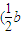 ,
,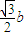 ,0),(0,0,a).
,0),(0,0,a).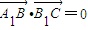 .
.
∴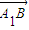 =
=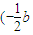 ,
,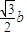 ,a),
,a),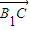 =
=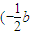 ,
,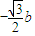 ,
,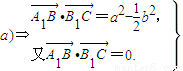
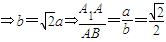 .
.
(2)在(1)条件下,不妨设b=2,则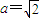 ,
,
又A,M,N坐标分别为(b,0,a),(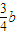 ,
,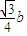 ,0),(
,0),(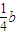 ,
,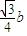 ,a).
,a).
∴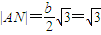 ,
,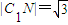 .∴
.∴
同理|AM|=|C1M|.
∴△AC1N与△AC1M均为以AC1为底边的等腰三角形,
取AC1中点为P,则NP⊥AC1,MP⊥AC1⇒∠NPM为二面角N-AC1-M的平面角,
而点P坐标为(1,0,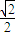 ),
),
∴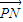 =
=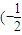 ,
,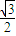 ,
,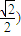 .同理
.同理 =
=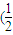 ,
,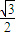 ,
,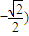 .
.
∴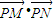 =
=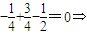
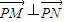 .
.
∴∠NPM=90°⇒二面角N-AC1-M的大小等于90°.
点评:本题主要考查了二面角及其度量,以及空间向量,考查空间想象能力、运算能力和推理论证能力,属于中档题.
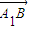 与
与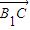 的坐标,根据
的坐标,根据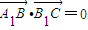 求出a与b的关系,从而求出
求出a与b的关系,从而求出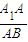 ,
,(2)在(1)条件下,不妨设b=2,则
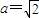 ,取AC1中点为P,根据二面角的平面角的定义可知∠NPM为二面角N-AC1-M的平面角,分别求出
,取AC1中点为P,根据二面角的平面角的定义可知∠NPM为二面角N-AC1-M的平面角,分别求出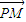 与
与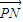 的坐标,计算它们的数量积即可求出此角.
的坐标,计算它们的数量积即可求出此角.解答:解:(1)以C1点为坐标原点,C1A1所在直线为x轴,C1C所在直线为z轴,建立空间直角坐标系,
设A1B1=b,AA1=a(a,b∈(0,+∞).
∵三棱柱ABC-A1B1C1为正三棱柱,则A1,B,B1,C的坐标分别为:
(b,0,0),
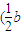 ,
,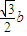 ,a),
,a),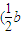 ,
,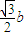 ,0),(0,0,a).
,0),(0,0,a).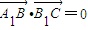 .
.∴
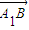 =
=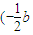 ,
,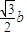 ,a),
,a),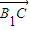 =
=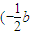 ,
,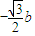 ,
,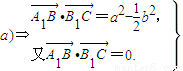
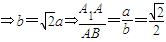 .
.(2)在(1)条件下,不妨设b=2,则
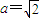 ,
,又A,M,N坐标分别为(b,0,a),(
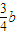 ,
,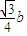 ,0),(
,0),(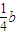 ,
,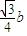 ,a).
,a).∴
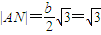 ,
,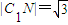 .∴
.∴
同理|AM|=|C1M|.
∴△AC1N与△AC1M均为以AC1为底边的等腰三角形,
取AC1中点为P,则NP⊥AC1,MP⊥AC1⇒∠NPM为二面角N-AC1-M的平面角,
而点P坐标为(1,0,
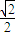 ),
),∴
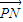 =
=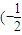 ,
,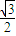 ,
,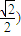 .同理
.同理 =
=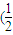 ,
,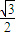 ,
,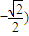 .
.∴
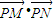 =
=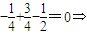
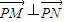 .
.∴∠NPM=90°⇒二面角N-AC1-M的大小等于90°.
点评:本题主要考查了二面角及其度量,以及空间向量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.