题目内容
两个具有线性相关关系的变量的一组数据为:
将以上数据,以x为自变量,y为因变量,得回归方程为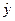 =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为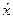 =b′y+a′.
=b′y+a′.
定义两个变量的相关关系数r的计算公式为r=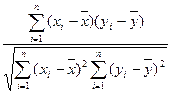 ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.
试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?
| 数据 | 1 | 2 | 3 | … | n |
| 变量x | x1 | x2 | x3 | … | xn |
| 变量y | y1 | y2 | y3 | … | yn |
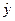 =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为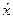 =b′y+a′.
=b′y+a′.定义两个变量的相关关系数r的计算公式为r=
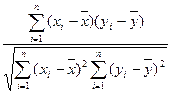 ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?
在方程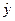 =bx+a中b=
=bx+a中b= ,在方程
,在方程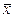 =b′y+a′中b′=
=b′y+a′中b′= ,
,
于是bb′= .
. =
=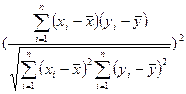 =r2.
=r2.
故r=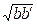 ,
,
即r能用b,b′表示,且r=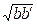 .
.
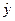 =bx+a中b=
=bx+a中b= ,在方程
,在方程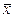 =b′y+a′中b′=
=b′y+a′中b′= ,
,于是bb′=
 .
. =
=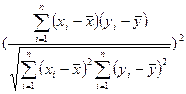 =r2.
=r2.故r=
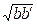 ,
,即r能用b,b′表示,且r=
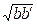 .
. 本题容易产生两个错答案
错解一:因为两组变量一旦确定后,两组变量间的相关关系也随之确定了,故r不是随b,a,b′,a′的变化而变化的,于是r不能用b,a及b′,a′表示.
错解二:因为b为回归方程的斜率,a为截距,斜率与截距的取值范围均为R,而相关系数r的取值范围为[-1,1],它们的取值范围不一样,因而r不能用b,a及b′,a′表示.
产生这种错解的原因是:当变量确定后,r是随之而确定了,但b,a及b′, a′也?随之而定了,上述错解一中视以上四个系数在变化,因而误认为r与它们无关而发生了错误.对于错解二,虽然对b与a及r的范围的说法均是正确的,但未曾注意到两个方程之间的相关关系,即系数b,a与b′,a′并不是两组完全独立的变量,因而也造成了解答的错误.
错解一:因为两组变量一旦确定后,两组变量间的相关关系也随之确定了,故r不是随b,a,b′,a′的变化而变化的,于是r不能用b,a及b′,a′表示.
错解二:因为b为回归方程的斜率,a为截距,斜率与截距的取值范围均为R,而相关系数r的取值范围为[-1,1],它们的取值范围不一样,因而r不能用b,a及b′,a′表示.
产生这种错解的原因是:当变量确定后,r是随之而确定了,但b,a及b′, a′也?随之而定了,上述错解一中视以上四个系数在变化,因而误认为r与它们无关而发生了错误.对于错解二,虽然对b与a及r的范围的说法均是正确的,但未曾注意到两个方程之间的相关关系,即系数b,a与b′,a′并不是两组完全独立的变量,因而也造成了解答的错误.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
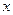
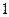
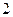


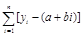 最小
最小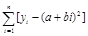 最小
最小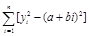 最
最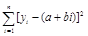 最小
最小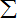
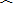
 叙述正确的是( )
叙述正确的是( ) ,且
,且 越大,相关程度越大.
越大,相关程度越大.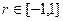 ,且
,且