题目内容
解答题
已知a＋b＝1，a、b∈R+，求证：a4＋b4≥
．
答案：
解析：
解析：
|
证明：配方得a4＋b4＝(a2＋b2)2－2a2b2＝[(a＋b)2－2ab]2－2a2b2＝(1－2ab)2－2a2b2． ∵a＋b≥2 ∴1≥4ab，ab≤ 又a2b2≤ ∴(1－2ab)2－2a2b2≥ 即a4＋b4≥ |
，
，1－2ab≥
，(1－2ab)2≥
，
，－2a2b2≥－
．
－
＝
．
练习册系列答案
全优点练单元计划系列答案
相关题目
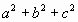＝3，求证：－
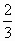＜b＋c＜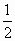
．
．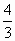