题目内容
解答题
已知a,b,c均为实数,函数f(x)=ax2+bx+c与g(x)=ax+b,且当-1≤x≤1时,恒有|f(x)|≤1.证明:(1)|c|≤1;(2)|g(x)|≤2.
答案:
解析:
解析:
|
①令x=0,则f(0)=c. ∵当-1≤x≤1时,|f(x)|≤1,∴|c|≤1. ②当a>0,g(x)=ax+b在[-1,1]上是增函数, ∴g(-1)≤g(x)≤g(1). ∵|f(x)|≤1,|c|≤1,(当-1≤x≤1时), ∴g(1)=a+b=f(1)-c≤|f(1)|+|c|≤2, g(-1)=-a+b=-f(-1)+c≥-(|f(1)+|c|)≥-2, ∴-2≤g(x)≤2,∴|g(x)|≤2. 当a<0时,g(x)在[-1,1]上是减函数. ∴g(1)≤g(x)≤g(-1). ∵|f(x)|≤1,|c|≤1(当-1≤x≤1时) ∴g(-1)=-a+b=-f(-1)+c≤|f(-1)|+|c|≤2, g(1)=a+b=f(1)-c≥-(|f(1)|+|c|)≥-2, ∴-2≤g(x)≤2,∴|g(x)|≤2. 综合以上,|g(x)|≤2. |

练习册系列答案
相关题目
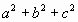 =3,求证:-
=3,求证:-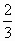 <b+c<
<b+c<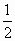 .
.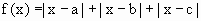 的最小值.
的最小值.