题目内容
已知a,b为不相等的正数,且a3-b3=a2-b2.
求证:1<a+b<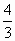 .
.
答案:
解析:
解析:
|
证明:先证a+b>1. 因为a,b为不相等的正数,所以a-b≠0.由已知a3-b3=a2-b2,所以a2+ab+b2=a+b.所以(a+b)2=a2+2ab+b2>a2+ab+b2=a+b.故a+b>1. 再证a+b< 只需证:3(a+b)<4,只需证:3(a+b)2<4(a+b)=4(a2+ab+b2),只需证:a2-2ab+b2>0,因为a≠b,所以(a-b)2>0恒成立.所以a+b< |

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
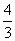 .
.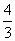 ,故命题得证.
,故命题得证.