题目内容
解答题
已知a,b,c为三角形三边,x,y,z为不全为零的实数,且x+y+z=0,求证:a2yz+b3xz+c2xy<0.
答案:
解析:
解析:
|
证法一:由已知z=-x-y,代入原不等式得xy·(c2-a2-b2)<a2y2+b2x2, 故只需证-2abxy·cosC<a2y2+b2x2, 而2ab|xy|<a2y2+b2x2,|cosC|<1, ∴-2abxy·cosC<a2y2+b2x2成立. 从而原不等式成立. 证法二:在△ABC中,有|c2-a2-b2|=|2abcosC|<2ab. 由基本不等式,得a2y2+b2x2≥2ab|xy|>2ab|xy||cosC|≥-2abxycosC=xy(c2-a2-b2). 即0>a2y(-x-y)+b2x(-x-y)+c2xy=a2yz+b2xz+c2xy. ∴a2yz+b2xz+c2xy<0. |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
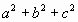 =3,求证:-
=3,求证:-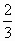 <b+c<
<b+c<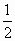 .
.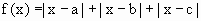 的最小值.
的最小值.