题目内容
若抛物线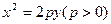 的焦点与椭圆
的焦点与椭圆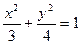 的上焦点重合,
的上焦点重合,
1)求抛物线方程.
2)若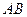 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线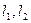 是抛物线两条分别切于
是抛物线两条分别切于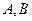 的切线,求
的切线,求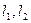 的交点的纵坐标.(12分)
的交点的纵坐标.(12分)
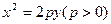 的焦点与椭圆
的焦点与椭圆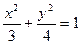 的上焦点重合,
的上焦点重合,1)求抛物线方程.
2)若
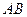 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线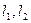 是抛物线两条分别切于
是抛物线两条分别切于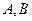 的切线,求
的切线,求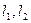 的交点的纵坐标.(12分)
的交点的纵坐标.(12分)(1)
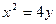
(2)
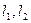 的交点的纵坐标为-1.
的交点的纵坐标为-1.解:
1)抛物线的方程为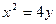
2)设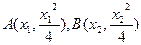
设以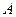 为切点的切线的斜率为
为切点的切线的斜率为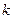 (
(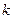 存在,
存在,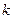 不存在显然不符题意),则切线为
不存在显然不符题意),则切线为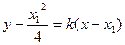 与
与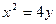 联立,利用判别式为0,则
联立,利用判别式为0,则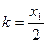 ,同理以
,同理以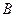 为切点的切线的斜率为
为切点的切线的斜率为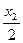 ,
,
于是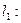
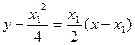 -----①
-----①
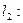
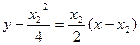 ----②
----②
①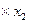 -②
-②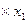 可得
可得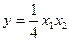
因为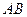 过焦点(0,1),所以设
过焦点(0,1),所以设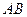 方程为
方程为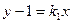 (
(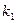 存在,
存在,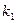 不存在显然不符题意),
不存在显然不符题意),
与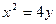 联立得
联立得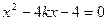 ,所以
,所以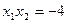 ,于是
,于是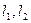 的交点的纵坐标为-1.
的交点的纵坐标为-1.
1)抛物线的方程为
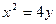
2)设
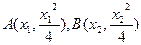
设以
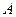 为切点的切线的斜率为
为切点的切线的斜率为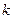 (
(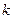 存在,
存在,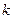 不存在显然不符题意),则切线为
不存在显然不符题意),则切线为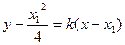 与
与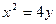 联立,利用判别式为0,则
联立,利用判别式为0,则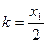 ,同理以
,同理以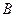 为切点的切线的斜率为
为切点的切线的斜率为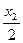 ,
,于是
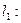
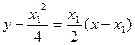 -----①
-----①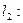
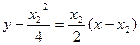 ----②
----②①
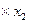 -②
-②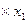 可得
可得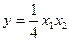
因为
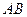 过焦点(0,1),所以设
过焦点(0,1),所以设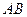 方程为
方程为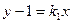 (
(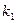 存在,
存在,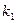 不存在显然不符题意),
不存在显然不符题意),与
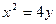 联立得
联立得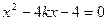 ,所以
,所以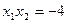 ,于是
,于是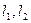 的交点的纵坐标为-1.
的交点的纵坐标为-1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
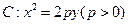 截得的弦长为
截得的弦长为 。
。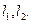
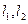 交于点M,求直线AB的方程;
交于点M,求直线AB的方程;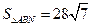 时,求点N的坐标
时,求点N的坐标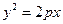 x上横坐标为4的点到该抛物线的焦点的距离为5。
x上横坐标为4的点到该抛物线的焦点的距离为5。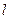 交抛物线C于A、B两点,求证:
交抛物线C于A、B两点,求证: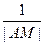 +
+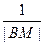 恒为定值。
恒为定值。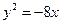 的焦点坐标是( )
的焦点坐标是( )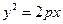 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则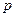 的值为___________
的值为___________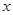 轴上的抛物线被直线
轴上的抛物线被直线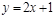 截得的弦长为
截得的弦长为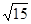 ,求抛物线的方程。
,求抛物线的方程。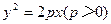 的焦点F的直线
的焦点F的直线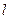 交抛物线于A、B,交其准线于点C,若
交抛物线于A、B,交其准线于点C,若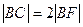 且
且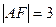 ,则此抛物线的方程为( )
,则此抛物线的方程为( )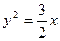 B.
B.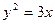 C.
C.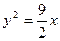 D.
D.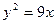
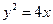 内一点
内一点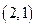 的弦被该点平分,则该弦所在直线方程是
的弦被该点平分,则该弦所在直线方程是 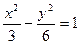 的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A、B两点。
的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A、B两点。