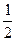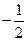题目内容
(本小题满分12分)在平面直角坐标系xoy中,已知抛物线C: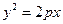 x上横坐标为4的点到该抛物线的焦点的距离为5。
x上横坐标为4的点到该抛物线的焦点的距离为5。
(1)求抛物线C的标准方程;
(2)过点M(1,0)作直线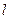 交抛物线C于A、B两点,求证:
交抛物线C于A、B两点,求证: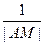 +
+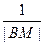 恒为定值。
恒为定值。
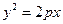 x上横坐标为4的点到该抛物线的焦点的距离为5。
x上横坐标为4的点到该抛物线的焦点的距离为5。(1)求抛物线C的标准方程;
(2)过点M(1,0)作直线
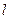 交抛物线C于A、B两点,求证:
交抛物线C于A、B两点,求证: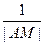 +
+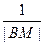 恒为定值。
恒为定值。(1)
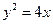
(2)略
解:(1)依题意得: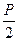 +4="5 " ∴P="2"
+4="5 " ∴P="2"
∴抛物线C标准方程为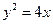 (4分)
(4分)
(2)当l斜率不存在时,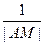 +
+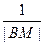 =
=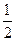 +
+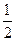 ="1 " (6分)
="1 " (6分)
当l斜率存在时,设l直线方程为:y=k(x-1)(k≠0)代入y2=4x
得 k2x2-(2k2+4)x+k2=0
k2x2-(2k2+4)x+k2=0
设A(x1,y1),B(x2,y2)则x1+x 2=
2=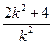 , x1x2=1
, x1x2=1
∴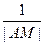 +
+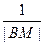 =
=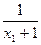 +
+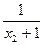 =
=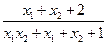 ="1 " (10分)
="1 " (10分)
综上得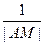 +
+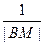 恒为定值1。 (12分)
恒为定值1。 (12分)
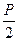 +4="5 " ∴P="2"
+4="5 " ∴P="2" ∴抛物线C标准方程为
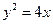 (4分)
(4分)(2)当l斜率不存在时,
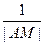 +
+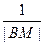 =
=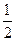 +
+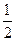 ="1 " (6分)
="1 " (6分)当l斜率存在时,设l直线方程为:y=k(x-1)(k≠0)代入y2=4x
得
 k2x2-(2k2+4)x+k2=0
k2x2-(2k2+4)x+k2=0设A(x1,y1),B(x2,y2)则x1+x
 2=
2=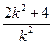 , x1x2=1
, x1x2=1∴
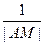 +
+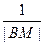 =
=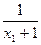 +
+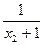 =
=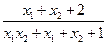 ="1 " (10分)
="1 " (10分)综上得
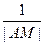 +
+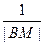 恒为定值1。 (12分)
恒为定值1。 (12分)
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 分)已知抛物线的顶点在坐标原点,焦点在
分)已知抛物线的顶点在坐标原点,焦点在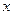 轴正半轴,抛物线上一点
轴正半轴,抛物线上一点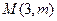 到焦点的距离为
到焦点的距离为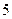 ,求
,求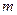 的值及抛物线方程.
的值及抛物线方程. 的焦点坐标为( )
的焦点坐标为( ) ,0)
,0) )
)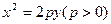 的焦点与椭圆
的焦点与椭圆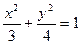 的上焦点重合,
的上焦点重合,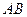 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线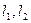 是抛物线两条分别切于
是抛物线两条分别切于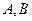 的切线,求
的切线,求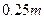 ,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到
,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到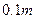 )
)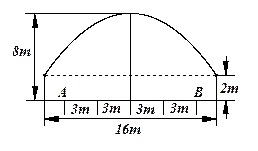
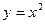 上的点,若过点P的切线方程与直线
上的点,若过点P的切线方程与直线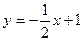 垂直,则过P点处的切线方程是____________.
垂直,则过P点处的切线方程是____________.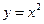 的焦点坐标为 ( )
的焦点坐标为 ( )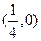 B
B 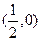 C
C  D
D 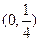
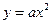 在点(1,a)处的切线与直线
在点(1,a)处的切线与直线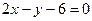 平行,则a=
平行,则a=