题目内容
(本小题满分13分)
袋中装着标有数字1,2,3,4的小球各3个,从袋中任取3个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字互不相同的概率;
(Ⅱ)用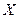 表示取出的3个小球上所标的最大数字,求随机变量
表示取出的3个小球上所标的最大数字,求随机变量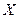 的分布列和均值.
的分布列和均值.
袋中装着标有数字1,2,3,4的小球各3个,从袋中任取3个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字互不相同的概率;
(Ⅱ)用
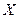 表示取出的3个小球上所标的最大数字,求随机变量
表示取出的3个小球上所标的最大数字,求随机变量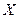 的分布列和均值.
的分布列和均值.(1)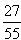 (2)
(2)
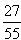 (2)
(2)
(I)“一次取出的3个小球上的数字互不相同”的事件记为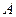 ,
,
则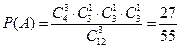 .…………………………………………………5分
.…………………………………………………5分
(II)由题意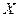 所有可能的取值为:
所有可能的取值为: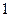 ,
,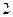 ,
,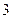 ,
,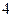 .…………………………………6分
.…………………………………6分
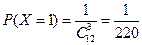 ;
;
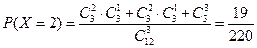 ;
;
 ;
;
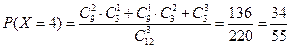 .
.
所以随机变量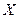 的分布列为
的分布列为
……………………………………………………………10分
随机变量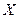 的均值为
的均值为
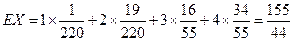 .………………………………13分
.………………………………13分
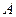 ,
,则
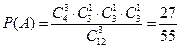 .…………………………………………………5分
.…………………………………………………5分(II)由题意
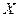 所有可能的取值为:
所有可能的取值为: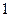 ,
,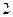 ,
,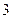 ,
,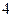 .…………………………………6分
.…………………………………6分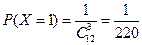 ;
;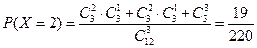 ;
; ;
;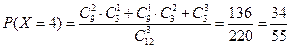 .
.所以随机变量
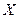 的分布列为
的分布列为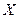 | 1 | 2 | 3 | 4 |
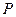 | 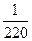 | 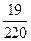 | 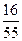 | 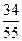 |
随机变量
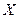 的均值为
的均值为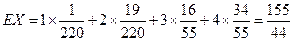 .………………………………13分
.………………………………13分
练习册系列答案
相关题目
 的所有非空真子集中等可能地取出一个.
的所有非空真子集中等可能地取出一个. 比数列的概率;
比数列的概率; ,求
,求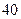 名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.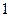
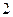
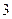
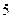
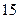
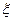 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量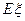 .
.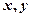 ,设
,设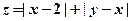 ,
,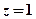 ”发生的概
”发生的概 率;
率;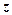 的最大值,并求事件“
的最大值,并求事件“ ,
, 分别表示甲乙所得的点数,记
分别表示甲乙所得的点数,记 ,用
,用 表示“点
表示“点 内的事件”求事件
内的事件”求事件 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。 满足:
满足: ,则
,则 的值是 ( )
的值是 ( )



 ~
~ ,则
,则 的最大值为 .
的最大值为 . 学科
学科


