题目内容
（极坐标与参数方程选做题）在极坐标系中，已知A（1，0）B（1，
）点P在曲线ρcos2θ+4cosθ=ρ上，则|PA|+|PB|最小值为
．
| π |
| 2 |
| 2 |
| 2 |
分析：先求得曲线ρcos2θ+4cosθ=ρ 的直角坐标方程 y2=4x，表示一条抛物线，焦点为A（1，0），数形结合可得|PA|+|PB|最小等于|AB|．
解答：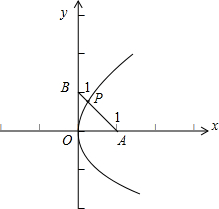
解：曲线ρcos2θ+4cosθ=ρ，即 （ρcosθ）2+4ρcosθ=ρ2，
化为直角坐标方程为 x2+4x=x2+y2，即 y2=4x，
表示一条抛物线，焦点为A（1，0）．
再根据点B的直角坐标为（0，1），点P在抛物线上，故当P为线段AB和抛物线的交点时，
|PA|+|PB|最小，且等于|AB|=
，
故答案为
．
解：曲线ρcos2θ+4cosθ=ρ，即 （ρcosθ）2+4ρcosθ=ρ2，化为直角坐标方程为 x2+4x=x2+y2，即 y2=4x，
表示一条抛物线，焦点为A（1，0）．
再根据点B的直角坐标为（0，1），点P在抛物线上，故当P为线段AB和抛物线的交点时，
|PA|+|PB|最小，且等于|AB|=
| 2 |
故答案为
| 2 |
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，抛物线的标准方程和简单性质，属于基础题．
练习册系列答案
相关题目
A．（不等式选讲选做题）函数y=|x+1|+|x-1|的最小值是