题目内容
 A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是
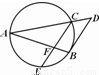
A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是B.(几何证明选讲选做题)如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针转60°到OD,则PD的长为
C.(极坐标与参数方程选做题)在极坐标系中,过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程为
分析:A 利用绝对值得意义,可得函数y=|x+1|+|x-1|的最小值等于2.
B 在Rt△OAB中,先求出∠AOB,从而得到∠DOP,△DOP 中,由余弦定理求得DP的长度.
C 求出 圆ρ 的普通方程,求出圆心,得到所求的直线方程,再把方程化为极坐标方程.
B 在Rt△OAB中,先求出∠AOB,从而得到∠DOP,△DOP 中,由余弦定理求得DP的长度.
C 求出 圆ρ 的普通方程,求出圆心,得到所求的直线方程,再把方程化为极坐标方程.
解答:解:A 函数y=|x+1|+|x-1|表示数轴上的x到-1和1的距离之和,故 函数y=|x+1|+|x-1|的最小值等于2.
B 在Rt△OAB中,COS∠AOB=
=
,∴∠AOB=60°∠DOP=∠AOB+∠DOA=60°+60°=120°,
△DOP 中,由余弦定理得 PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2(-
)=7,
∴DP=
.
C 圆ρ=6cosθ的普通方程为 x2+y2=6x,表示圆心为(3,0),半径等于3的圆,
故过圆ρ=6cosθ的圆心,且垂直于极轴的直线为 x=3,∴极坐标方程为 ρcosθ=3.
故答案为:2;
;ρcosθ=3.
B 在Rt△OAB中,COS∠AOB=
| OA |
| OP |
| 1 |
| 2 |
△DOP 中,由余弦定理得 PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2(-
| 1 |
| 2 |
∴DP=
| 7 |
C 圆ρ=6cosθ的普通方程为 x2+y2=6x,表示圆心为(3,0),半径等于3的圆,
故过圆ρ=6cosθ的圆心,且垂直于极轴的直线为 x=3,∴极坐标方程为 ρcosθ=3.
故答案为:2;
| 7 |
点评:本题考查绝对值得意义,直角三角形中的边角关系、余弦定理的应用,极坐标方程与普通方程的互化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则线段CD的长为 .
,则线段CD的长为 .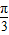 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .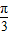 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .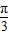 )的直角坐标是 .
)的直角坐标是 .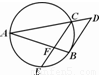
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .