题目内容
(本题13分)
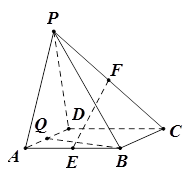
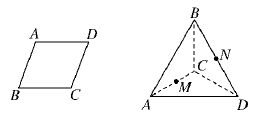
如图,在四棱锥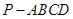 中,
中,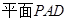
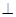 平面
平面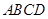 ,底面
,底面 是菱形,
是菱形,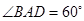 .
.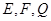 分别是
分别是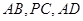 的中点.
的中点.
(1) 求证: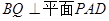 ;
;
(2) 求证: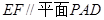 .
.
如图,在四棱锥
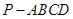 中,
中,
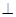 平面
平面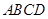 ,底面
,底面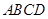 是菱形,
是菱形,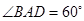 .
.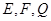 分别是
分别是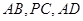 的中点.
的中点.
(1) 求证:
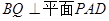 ;
;(2) 求证:
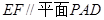 .
.(1)先证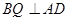 ,根据面面垂直的性质定理可知
,根据面面垂直的性质定理可知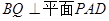
(2)先证FG//AE,且FG=AE,再证AG//EF,根据线面平行的判定定理可证.
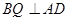 ,根据面面垂直的性质定理可知
,根据面面垂直的性质定理可知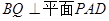
(2)先证FG//AE,且FG=AE,再证AG//EF,根据线面平行的判定定理可证.
试题分析:(1)在菱形ABCD中
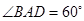 ,所以,AB=BD,
,所以,AB=BD,因为Q是AD的中点,
所以
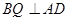 ,且
,且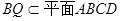 ,
,又因为,平面PAD
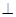 平面ABCD,平面PAD
平面ABCD,平面PAD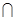 平面ABCD=AD,
平面ABCD=AD,所以
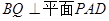 . ……6分
. ……6分(2)取PD中点G,连接AG,FG,
因为E、F分别是AB,PC中点,
所以FG//AE,且FG=AE,
所以,四边形AEFG为平行四边形,所以,AG//EF
又因为
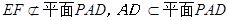
所以
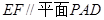 。 ……13分
。 ……13分点评:要证明线面垂直和线面平行,要紧扣相应的定理的条件,定理中的条件要一一列出来,缺一不可.

练习册系列答案
相关题目
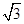 ,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为
,∠BAC=120°,若点P为△ABC内的动点满足直线DP与平面ABC所成角的正切值为2,则点P在△ABC内所成的轨迹的长度为 
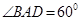 且边长是2的菱形
且边长是2的菱形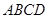 ,沿它的对角线
,沿它的对角线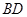 折成60°的二面角,则( )
折成60°的二面角,则( )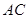 与
与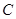 到平面
到平面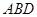 的距离是 .
的距离是 .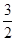
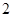
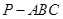 中,
中,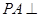 底面
底面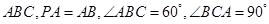 ,点
,点 ,
,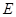 分别在棱
分别在棱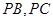 上,且
上,且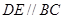
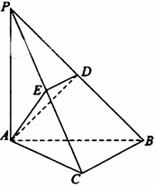
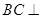 平面
平面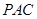 ;
;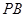 的中点时,求
的中点时,求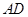 与平面
与平面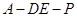 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.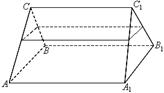
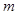 、
、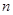 为两条不重合的直线,
为两条不重合的直线,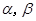 为两个不重合的平面,下列命题中正确命题的是
为两个不重合的平面,下列命题中正确命题的是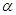 所成的角相等,则
所成的角相等,则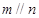
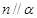 ,
,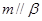 ,
,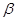 ,则
,则 ,
,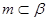 ,
,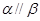
 ,
,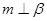 ,
,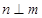
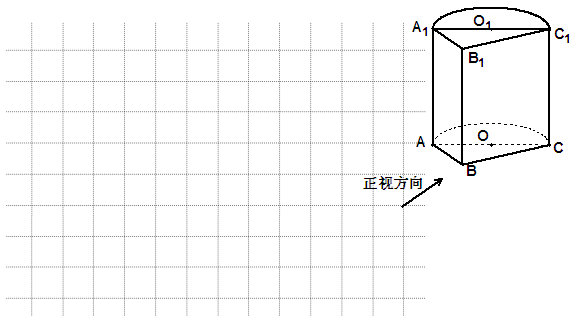
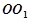 与三棱柱
与三棱柱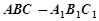 的组合体,其中,圆柱
的组合体,其中,圆柱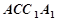 是边长为4的正方形,
是边长为4的正方形,
 为等腰直角三角形,
为等腰直角三角形, .
.
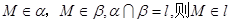 ;(4)空间中,相交于同一点的三条直线在同一平面内。
;(4)空间中,相交于同一点的三条直线在同一平面内。