题目内容
下面四个计算题中,结果正确的是 .(填序号)①若
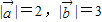 ,且
,且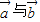 的夹角为60,则
的夹角为60,则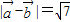 ;
;②棱长为2正方体ABCD-A1B1C1D1中,点A到平面BDD1B1的距离为d,则
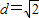 ;
;③棱长都是1的平行六面体ABCD-A1B1C1D1中,
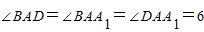 ,则对角线的长
,则对角线的长 ;
;④在120的二面角α-AB-β中AC?α,BD?β,AB⊥AC,AB⊥BD,AB=AC=BD=1,则点C与D的距离
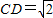 .
.
【答案】分析:利用平方法,可由已知求出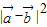 ,进而求出
,进而求出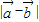 ,判断出①的真假;
,判断出①的真假;
根据正方体的几何特征,可得A与底面中心的之间的距离即为A到对角面的距离,进而判断出②的真假;
利用余弦定理和三余弦定理,求出棱长都是1且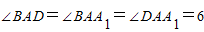 的平行六面体ABCD-A1B1C1D1的对角线AC1的长,进而判断③的真假;
的平行六面体ABCD-A1B1C1D1的对角线AC1的长,进而判断③的真假;
利用异面直线上两点之间距离公式,求出CD的长,可判断④的真假.
解答:解:∵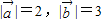 ,且
,且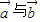 的夹角为60,∴
的夹角为60,∴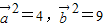 ,
,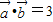 ,则
,则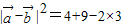 =7,则
=7,则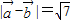 ;
;
连接AC,BD,交点为O,由正方体的几何特征可得d=OA= AB=
AB=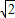 ;
;
棱长都是1的平行六面体ABCD-A1B1C1D1中,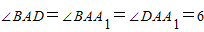 ,则AC=
,则AC=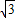 ,cos∠ACC1=-
,cos∠ACC1=-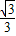 ,由余弦定理可得,对角线的长
,由余弦定理可得,对角线的长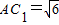 ;
;
在120的二面角α-AB-β中AC?α,BD?β,AB⊥AC,AB⊥BD,AB=AC=BD=1,则点C与D的距离CD=2.
故答案为:①②③
点评:本题以命题的真假判断为载体,考查了向量的模,正方体的几何特征,平行六面体的几何特征,异面直线上两点间距离公式,计算量比较大,难度也比较大.
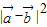 ,进而求出
,进而求出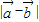 ,判断出①的真假;
,判断出①的真假;根据正方体的几何特征,可得A与底面中心的之间的距离即为A到对角面的距离,进而判断出②的真假;
利用余弦定理和三余弦定理,求出棱长都是1且
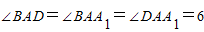 的平行六面体ABCD-A1B1C1D1的对角线AC1的长,进而判断③的真假;
的平行六面体ABCD-A1B1C1D1的对角线AC1的长,进而判断③的真假;利用异面直线上两点之间距离公式,求出CD的长,可判断④的真假.
解答:解:∵
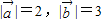 ,且
,且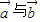 的夹角为60,∴
的夹角为60,∴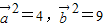 ,
,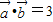 ,则
,则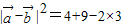 =7,则
=7,则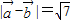 ;
;连接AC,BD,交点为O,由正方体的几何特征可得d=OA=
 AB=
AB=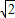 ;
;棱长都是1的平行六面体ABCD-A1B1C1D1中,
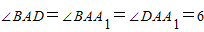 ,则AC=
,则AC=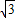 ,cos∠ACC1=-
,cos∠ACC1=-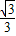 ,由余弦定理可得,对角线的长
,由余弦定理可得,对角线的长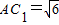 ;
;在120的二面角α-AB-β中AC?α,BD?β,AB⊥AC,AB⊥BD,AB=AC=BD=1,则点C与D的距离CD=2.
故答案为:①②③
点评:本题以命题的真假判断为载体,考查了向量的模,正方体的几何特征,平行六面体的几何特征,异面直线上两点间距离公式,计算量比较大,难度也比较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 [选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.
[选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分. 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)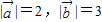 ,且
,且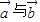 的夹角为60,则
的夹角为60,则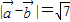 ;
;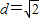 ;
;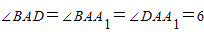 ,则对角线的长
,则对角线的长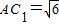 ;
;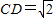 .
.