题目内容
(本小题满分12分)
如图,已知直线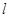 与抛物线
与抛物线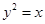 相交于
相交于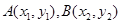 两点,
两点,
与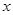 轴相交于点
轴相交于点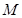 ,若
,若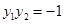 .
.
(1)求证: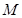 点的坐标为(1,0);
点的坐标为(1,0);
(2)求△AOB的面积的最小值.
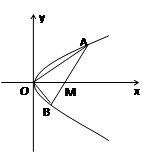
如图,已知直线
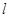 与抛物线
与抛物线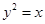 相交于
相交于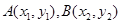 两点,
两点,与
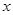 轴相交于点
轴相交于点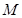 ,若
,若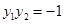 .
.(1)求证:
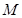 点的坐标为(1,0);
点的坐标为(1,0);(2)求△AOB的面积的最小值.

解:
(1) 设M点的坐标为(x0, 0), 直线l方程为 x =" my" + x0 ,
代入y2 = x得 y2-my-x0 =" 0 " ① y1、y2是此方程的两根,
∴ x0=-y1y2=1,即M点的坐标为(1, 0).
…………7分
(2)法一:
由方程①得y1+y2 =" m" ,y1y2=-1 ,且 | OM | = x0 =1,
于是S△AOB =
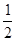 | OM | |y1-y2| =
| OM | |y1-y2| =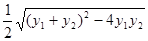 =
=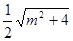 ≥1,
≥1,∴ 当m = 0时,△AOB的面积取最小值1. …………12分 法二:
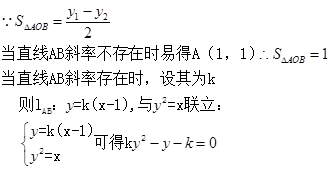
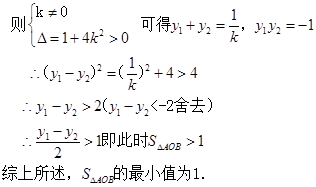
略

练习册系列答案
相关题目
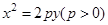 的焦点,另两个顶点在抛物线上,则满足此条件的正三角形共有
的焦点,另两个顶点在抛物线上,则满足此条件的正三角形共有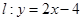 被抛物线C:
被抛物线C: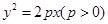 截得的弦长
截得的弦长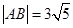 .
.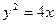 ,过点
,过点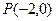 的直线AB交抛物线于点
的直线AB交抛物线于点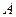 、
、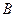 ,若线段
,若线段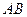 的垂直平分线交
的垂直平分线交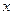 轴于点
轴于点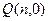 ,求
,求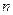 的取值范围.
的取值范围.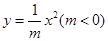 的焦点坐标是
的焦点坐标是 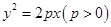 的焦点作倾斜角为
的焦点作倾斜角为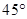 的直线交抛物线于
的直线交抛物线于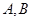 两点,若线段
两点,若线段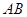 的中点坐标为
的中点坐标为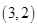 ,则
,则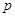 的值为( )
的值为( )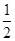
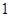

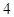
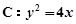 的焦点
的焦点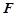 的直线l交抛物线C于
的直线l交抛物线C于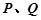 两点,若点P关于x轴对称的点为M,则直线QM的方程可能为
两点,若点P关于x轴对称的点为M,则直线QM的方程可能为 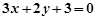


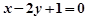
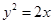 的焦点
的焦点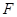 ,倾斜角为
,倾斜角为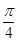 的直线
的直线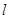 交抛物线于
交抛物线于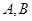 (
(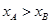 ),则
),则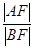 的值
的值 .
.