题目内容
数列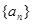 的前
的前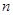 项和
项和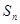 满足
满足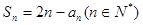 .
.
(1)计算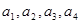 的值;
的值;
(2)猜想数列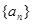 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.
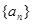 的前
的前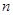 项和
项和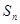 满足
满足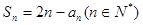 .
.(1)计算
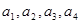 的值;
的值;(2)猜想数列
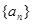 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.(1)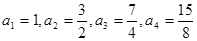 ;(2)见解析.
;(2)见解析.
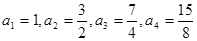 ;(2)见解析.
;(2)见解析.(1)根据前n项和的概念,把n的取值逐个代入即可求解;(2)先根据前几项猜想数列的通项,然后利用数学归纳法的步骤求证即可.
解:(1)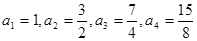 .…………4分
.…………4分
(2)猜想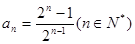 证明如下: …………5分
证明如下: …………5分
①当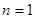 时,
时,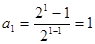 成立. ……………………6分
成立. ……………………6分
②假设当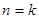 时成立,即
时成立,即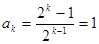 ,
,
则当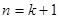 时,
时,
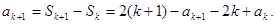 ……8分
……8分
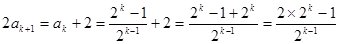
所以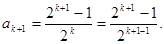
所以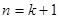 时结论也成立.………………………………10分
时结论也成立.………………………………10分
由①②知,对任意的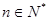 ,
,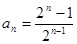 都成立.
都成立.
解:(1)
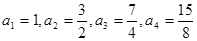 .…………4分
.…………4分(2)猜想
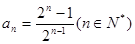 证明如下: …………5分
证明如下: …………5分①当
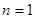 时,
时,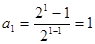 成立. ……………………6分
成立. ……………………6分②假设当
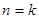 时成立,即
时成立,即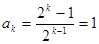 ,
,则当
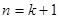 时,
时,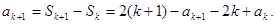 ……8分
……8分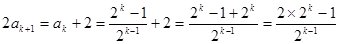
所以
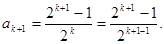
所以
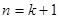 时结论也成立.………………………………10分
时结论也成立.………………………………10分由①②知,对任意的
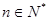 ,
,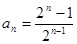 都成立.
都成立.
练习册系列答案
相关题目
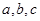 ,若
,若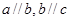 ,则
,则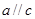 .类推出:向量
.类推出:向量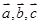 ,若
,若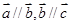 则
则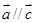
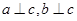 ,则
,则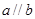 .类推出:空间中,三条不同的直线
.类推出:空间中,三条不同的直线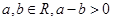 则
则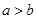 .类比出:任意
.类比出:任意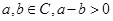 则
则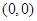 为圆心,
为圆心,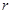 为半径的圆的方程是
为半径的圆的方程是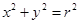 .类推出:以点
.类推出:以点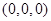 为球心,
为球心,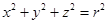
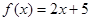 的图像是一条直线”这个推理所省略的大前提是
的图像是一条直线”这个推理所省略的大前提是 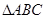 中,
中,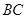 中点为
中点为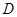 ,若
,若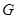 到各边的距离都相等,则
到各边的距离都相等,则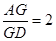 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体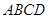 中,若
中,若 的中心为
的中心为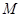 ,四面体内部一点
,四面体内部一点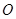 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则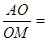 ( ▲ )
( ▲ )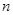 行
行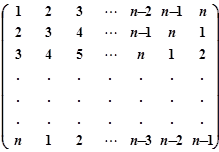
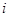 行第
行第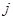 列的数为
列的数为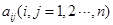 。
。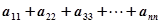 = ▲ ;(2分)
= ▲ ;(2分)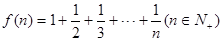 ,经计算的
,经计算的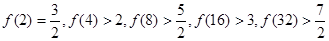 ,推测当
,推测当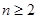 时,有__________________________.
时,有__________________________.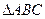 的三边长为
的三边长为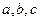 ,其内切圆半径为
,其内切圆半径为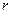 ,有结论:
,有结论: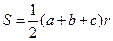 ,类比该结论,则在空间四面体
,类比该结论,则在空间四面体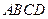 中,若四个面的面积分别为
中,若四个面的面积分别为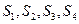 ,其内切球半径为
,其内切球半径为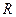 ,则有相应结论:____ ______.
,则有相应结论:____ ______.