题目内容
(1)如图,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求证:P,Q,R三点共线.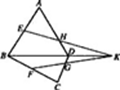
(2)如图,空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点, 且EH与FG相交于点K. 求证:EH,BD,FG三条直线相交于同一点.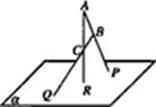
(1)详见解析;(2)详见解析.
解析试题分析:(1)由公理③可知,两个平面只要有一个公共点,则它们就有无数个公共点,且这些公共点共线,所以要证明三点共线,只需证明这三个点同时是两个平面的公共点;(2)要证明三条直线交于一点,只需证明其中的两条直线交于一点,再证明第三条直线也过交点,而证明点在一条直线上,只要说明直线是两个平面的交线,点是两个平面的公共点即可.
试题解析:(1)∵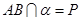 ,
,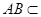 面
面 ∴
∴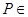 面
面 ,且
,且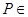 面
面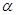 ,同理可证:
,同理可证: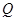
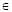 面
面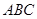 ,
,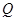
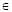 面
面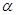 ;
;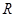
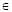 面
面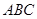 ,
,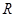
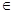 面
面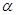 ,∴
,∴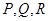 三点共线.
三点共线.
(2)∵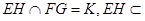 面
面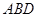 ,
,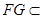 面
面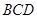 ,∴
,∴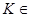 面
面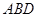 ,
,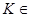 面
面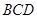 ,又面
,又面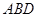 ∩面
∩面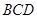 =
=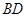 ,∴
,∴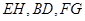 三条直线交于一点.
三条直线交于一点.
考点:平面的基本性质.

练习册系列答案
相关题目
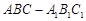 中,
中,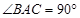 ,
,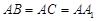 ,且
,且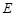 是
是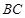 中点.
中点.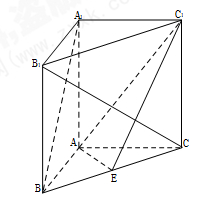
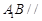 平面
平面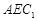 ;
;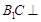 平面
平面 .
.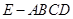 中,面
中,面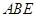
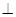 面
面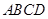 ,底面
,底面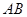 ∥
∥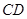 ,
,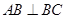 ,
,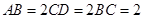 ,
,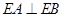 .
.
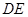 的位置关系;
的位置关系;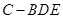 的体积;
的体积;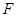 是线段
是线段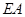 上一点,当
上一点,当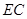 //平面
//平面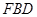 时,求
时,求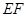 的长.
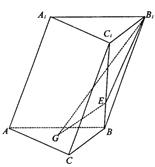
的长.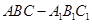 中,侧面
中,侧面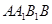 ⊥底面
⊥底面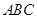 ,侧棱
,侧棱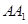 与底面
与底面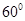 的角,
的角,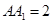 .底面
.底面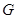 点,
点,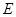 是线段
是线段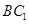 上一点,且
上一点,且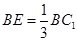 .
.
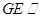 //侧面
//侧面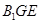 与底面
与底面 ,AD=1.
,AD=1.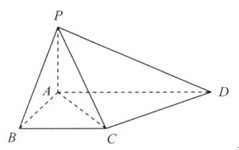
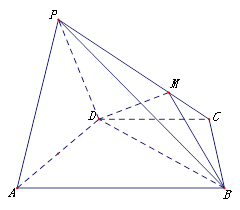
 中,平面
中,平面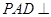 平面
平面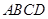 ,
,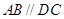 ,
,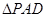 是等边三角形,已知
是等边三角形,已知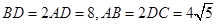 .
.
 是
是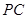 上的一点,证明:平面
上的一点,证明:平面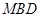 ;
;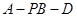 的余弦值.
的余弦值.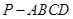 底面是平行四边形,面
底面是平行四边形,面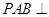 面
面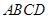 ,
,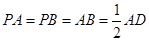 ,
,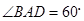 ,
,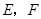 分别为
分别为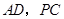 的中点.
的中点.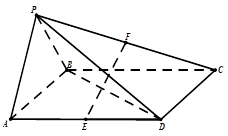
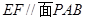 ;
; 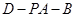 的余弦值.
的余弦值.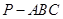 中,
中,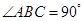 ,
,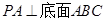
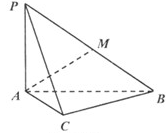
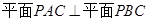 ;
;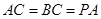 ,
,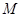 是
是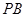 的中点,求
的中点,求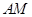 与平面
与平面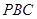 所成角的正切值
所成角的正切值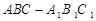 的底面是直角三角形,
的底面是直角三角形, 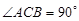 ,侧棱与底面所成角为
,侧棱与底面所成角为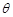 ,点
,点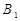 在底面上的射影
在底面上的射影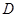 落在
落在 上.
上.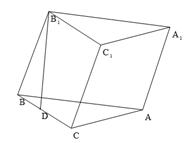
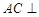 平面
平面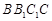 ;
;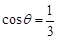 ,且当
,且当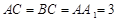 时,求二面角
时,求二面角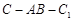 的大小.
的大小.