题目内容
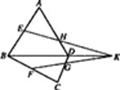
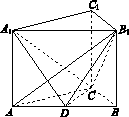
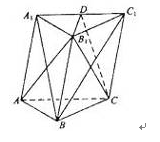
如图,在直三棱柱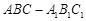 中,
中,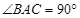 ,
,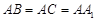 ,且
,且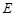 是
是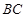 中点.
中点.
(I)求证: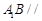 平面
平面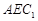 ;
;
(Ⅱ)求证: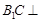 平面
平面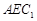 .
.
(Ⅰ)见解析;(Ⅱ)见解析.
解析试题分析:(Ⅰ)连接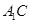 交
交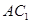 于点
于点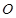 ,连接
,连接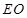 ,则可证
,则可证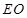 为
为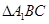 的中位线,则有
的中位线,则有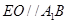 ,根据直线与平面平行的判定定理即知,
,根据直线与平面平行的判定定理即知,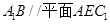 ;(Ⅱ)先由
;(Ⅱ)先由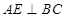 和
和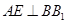 ,根据直线与平面垂直的判定定理可知,
,根据直线与平面垂直的判定定理可知,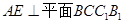 ,由直线与平面垂直的性质定理可知
,由直线与平面垂直的性质定理可知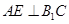 ;由角的与余切值相等得到
;由角的与余切值相等得到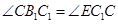 ,根据等量代换则有
,根据等量代换则有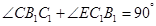 ,即
,即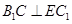 ,结合直线与平面垂直的判定定理可知,
,结合直线与平面垂直的判定定理可知, .
.
试题解析:(Ⅰ)连接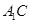 交
交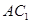 于点
于点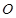 ,连接
,连接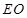 ,如图:
,如图: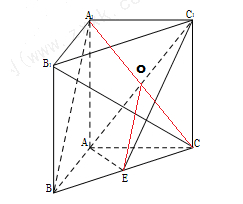
∵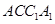 为正方形,∴
为正方形,∴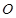 为
为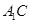 中点,
中点,
又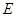 为
为 中点,∴
中点,∴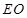 为
为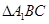 的中位线,
的中位线,
∴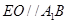 ,
,
又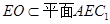 ,
,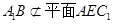 ,
,
∴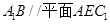 . 4分
. 4分
(Ⅱ)∵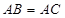 ,又
,又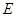 为
为 中点,∴
中点,∴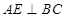 ,
,
又∵在直棱柱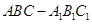 中,
中,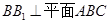 ,
,
又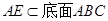 ,∴
,∴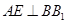 ,
,
又∵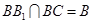 ,∴
,∴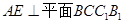 ,
,
又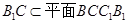 ,所以
,所以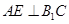 . 8分
. 8分
在矩形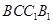 中,
中,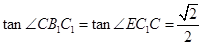 ,
,
∴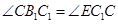 ,
,
∴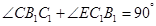 ,
,
即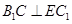 ,
,
又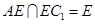 ,
,
∴ . 12分
. 12分
考点:1.直线与平面平行的判定定理;2.直线与平面垂直的判定定理;3.直线与平面垂直的性质定理

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
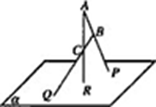
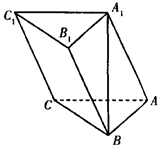
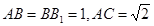 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.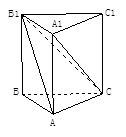
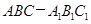 中,
中,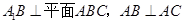 .
.
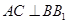 ;
;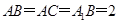 ,在棱
,在棱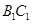 上确定一点P, 使二面角
上确定一点P, 使二面角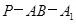 的平面角的余弦值为
的平面角的余弦值为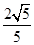 .
.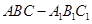 的侧面
的侧面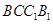 是菱形,
是菱形,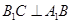
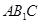
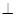 平面
平面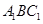 ;
;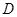 是
是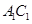 上的点,且
上的点,且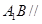 平面
平面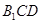 ,求
,求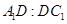 的值.
的值.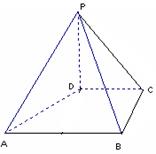
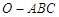 的侧棱
的侧棱 两两垂直,且
两两垂直,且 ,
,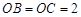 ,
, 是
是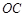 的中点。
的中点。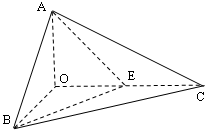
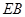 与
与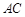 所成角的余弦值;
所成角的余弦值;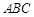 的所成角的正弦值。
的所成角的正弦值。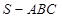 中,
中,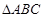 是边长为2的正三角形,平面
是边长为2的正三角形,平面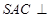 平面
平面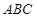 ,
,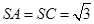 ,
,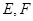 分别为
分别为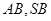 的中点.
的中点.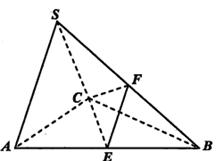
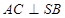 ;
; 的余弦值;
的余弦值;