题目内容
已知斜三棱柱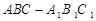 的底面是直角三角形,
的底面是直角三角形, 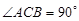 ,侧棱与底面所成角为
,侧棱与底面所成角为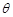 ,点
,点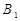 在底面上的射影
在底面上的射影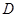 落在
落在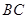 上.
上.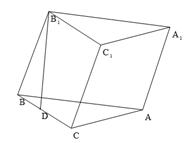
(1)求证: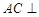 平面
平面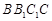 ;
;
(2)若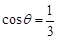 ,且当
,且当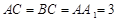 时,求二面角
时,求二面角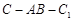 的大小.
的大小.
(1)详见解析;(2)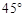 .
.
解析试题分析:(1)由 可得
可得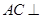 平面
平面 ;(2)建立空间直角坐标系,分别求出平面
;(2)建立空间直角坐标系,分别求出平面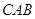 与平面
与平面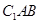 的法向量,利用
的法向量,利用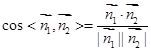 求解,注意坐标系的建立须准确,点、线的坐标表示正确.
求解,注意坐标系的建立须准确,点、线的坐标表示正确.
试题解析:(1)∵点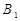 在底面上的射影
在底面上的射影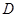 落在
落在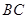 上,∴
上,∴ 平面
平面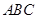 ,
,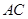
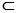 平面
平面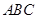 ,∴
,∴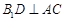 又∵
又∵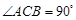 ∴
∴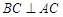 ,
,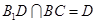 ,
,
∴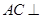 平面
平面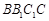 . 4分
. 4分
(2)∵ 平面
平面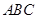 ∴
∴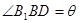 即
即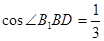
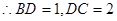
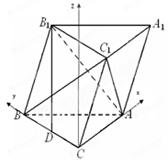
以 为原点,
为原点,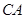 为x轴,
为x轴,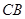 为
为 轴,过
轴,过 点且垂直于平面
点且垂直于平面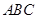 的直线为
的直线为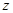 轴,
轴,
建立空间直角坐标系,则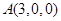 ,
,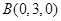 ,
,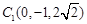 ,
,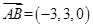 ,
, .显然,平面
.显然,平面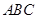 的法向量
的法向量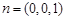 . 7分
. 7分
设平面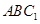 的法向量为
的法向量为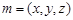 ,
,
由 ,即
,即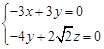 ,
,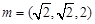 10分
10分
∴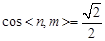 ,
, 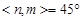
∴二面角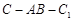 的大小是
的大小是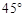 . 12分
. 12分
考点:1.线面垂直;2.二面角的求解;3.空间向量在立体几何中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

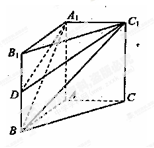
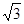 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小 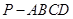 中,
中,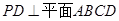 ,
,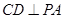 ,
, 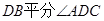 ,
,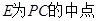 ,
,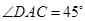 ,
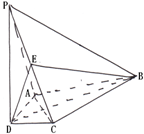
,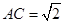 .
.
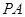 ∥
∥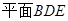 ;
;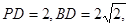 求四棱锥
求四棱锥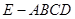 的体积
的体积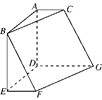
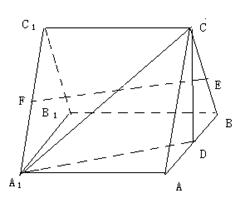
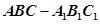 中,
中,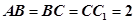 ,
,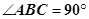 ,D是AC的中点.
,D是AC的中点.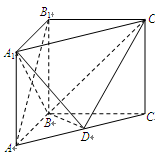
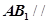 平面
平面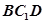 ;
;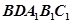 的体积.
的体积.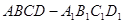 中,
中,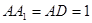 ,
,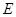 为
为 的中点,
的中点,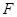 为
为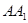 的中点.
的中点.
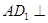 平面
平面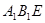 ;
;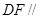 平面
平面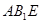 ;
;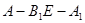 的大小为
的大小为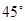 ,求
,求 的长.
的长.