题目内容
已知函数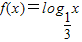 ,
,(1)当
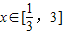 时,求f(x)的反函数g(x);
时,求f(x)的反函数g(x);(2)求关于x的函数y=[g(x)]2-2ag(x)+3(a≤3)当x∈[-1.1]时的最小值h(a);
(3)我们把同时满足下列两个性质的函数称为“和谐函数”:
①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间[p,q](p<q)使得函数在区间[p,q]上的值域为[p2,q2].
(Ⅰ)判断(2)中h(x)是否为“和谐函数”?若是,求出p,q的值或关系式;若不是,请说明理由;
(Ⅱ)若关于x的函数y=
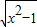 +t(x≥1)是“和谐函数”,求实数t的取值范围.
+t(x≥1)是“和谐函数”,求实数t的取值范围.
【答案】分析:(1)将f(x)看成关于x的方程,求出x,将x,y互换得到g(x).
(2)通过换元,将函数转化为关于t的二次函数,求出对称轴,通过对对称轴与区间位置关系的讨论,求出最小值g(a).
(3)据和谐函数的定义,列出方程组,求出p,q满足的条件.
解答:解:(1)由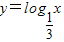 得
得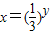
∴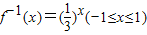
(2)令t=f-1(x),x∈[-1,1].由(1)知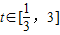 .
.
∴函数y=[f-1(x)]2-2a[f-1(x)]+3=t2-2at+3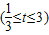
对称轴x=a(a≤3)
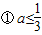 时,
时,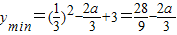
②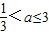 ,ymin=a2-2a2+3=3-a2.
,ymin=a2-2a2+3=3-a2.
∴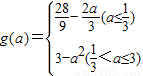 .
.
(3)对(2)中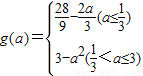 ,
,
易知g(x)在(-∞,3]上单减.
(3)(I)若g(x)为“和谐函数”,则g(x)在(-∞,3]上存在区间[p,q](p<q),使得g(x)在区间[p,q]
上的值域为[p2,q2].
①若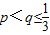 ,g(x)递减,
,g(x)递减,
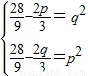 得p+q=
得p+q= ,
,
这与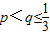 矛盾.
矛盾.
②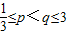 时
时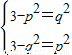 恒成立
恒成立
此时p、q、满足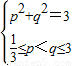 ,这样的p,q存在.
,这样的p,q存在.
③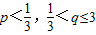 时,解得
时,解得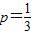 矛盾
矛盾
∴(2)中g(x)是“和谐函数”,p、q满足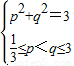
(II)∵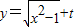 在[1,+∞)递增,有和谐函数的定义知,该函数在定义域[1,+∞)内,存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2]
在[1,+∞)递增,有和谐函数的定义知,该函数在定义域[1,+∞)内,存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2]
点评:本题考查新定义题,关键是理解透题中的新定义,此题型是近几年高考常考题型.求分段函数的函数值关键是判断出自变量所属的范围.
(2)通过换元,将函数转化为关于t的二次函数,求出对称轴,通过对对称轴与区间位置关系的讨论,求出最小值g(a).
(3)据和谐函数的定义,列出方程组,求出p,q满足的条件.
解答:解:(1)由
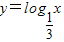 得
得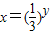
∴
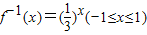
(2)令t=f-1(x),x∈[-1,1].由(1)知
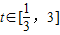 .
.∴函数y=[f-1(x)]2-2a[f-1(x)]+3=t2-2at+3
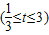
对称轴x=a(a≤3)
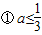 时,
时,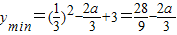
②
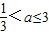 ,ymin=a2-2a2+3=3-a2.
,ymin=a2-2a2+3=3-a2.∴
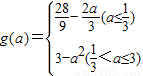 .
.(3)对(2)中
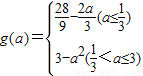 ,
,易知g(x)在(-∞,3]上单减.
(3)(I)若g(x)为“和谐函数”,则g(x)在(-∞,3]上存在区间[p,q](p<q),使得g(x)在区间[p,q]
上的值域为[p2,q2].
①若
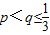 ,g(x)递减,
,g(x)递减,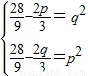 得p+q=
得p+q= ,
,这与
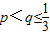 矛盾.
矛盾.②
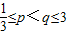 时
时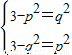 恒成立
恒成立此时p、q、满足
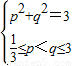 ,这样的p,q存在.
,这样的p,q存在.③
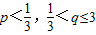 时,解得
时,解得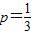 矛盾
矛盾 ∴(2)中g(x)是“和谐函数”,p、q满足
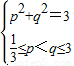
(II)∵
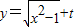 在[1,+∞)递增,有和谐函数的定义知,该函数在定义域[1,+∞)内,存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2]
在[1,+∞)递增,有和谐函数的定义知,该函数在定义域[1,+∞)内,存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2]点评:本题考查新定义题,关键是理解透题中的新定义,此题型是近几年高考常考题型.求分段函数的函数值关键是判断出自变量所属的范围.

练习册系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求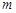 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).