题目内容
13.在△ABC中,内角A,B,C所对的边分别是a,b,c,b=10,c=16,C=2B,则cosC等于( )| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | ±$\frac{7}{25}$ | D. | $\frac{24}{25}$ |
分析 根据正弦定理可知$\frac{b}{sinB}=\frac{c}{sinC}=\frac{c}{sin2B}=\frac{c}{2sinBcosB}$,利用二倍角公式,即可求得结果.
解答 解:∵b=10,c=16,C=2B,
根据正弦定理可知,$\frac{b}{sinB}=\frac{c}{sinC}=\frac{c}{sin2B}=\frac{c}{2sinBcosB}$,
∴cosB=$\frac{c}{2b}$=$\frac{4}{5}$,
∴cosC=cos2B=2cos2B-1=2×($\frac{4}{5}$)2-1=$\frac{7}{25}$,
故选:A.
点评 本题考查了正弦定理和二倍角公式的应用,属于基本知识的考查.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
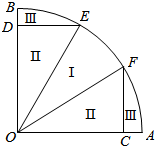 现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、
现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、