题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的偶函数,且
上的偶函数,且![]() 时,
时,![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求函数![]() 的解析式;
的解析式;
(3)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)0,-1
(2)![]()
(3)![]()
【解析】
试题(1)代入x的值,求出函数值即可;
(2)根据函数的奇偶性求出函数的解析式即可;
(3)通过讨论a的范围,得到关于a的不等式,解出即可.
试题解析:
(1)因为当x≤0时,f(x)=log![]() (-x+1),
(-x+1),
所以f(0)=0.
又因为函数f(x)是定义在R上的偶函数,
所以f(1)=f(-1)=log![]() [-(-1)+1]=log
[-(-1)+1]=log![]() 2=-1,
2=-1,
即f(1)=-1.
(2)令x>0,则-x<0,
从而f(-x)=log![]() (x+1)=f(x),
(x+1)=f(x),
∴x>0时,f(x)=log![]() (x+1).
(x+1).
∴函数f(x)的解析式为f(x)=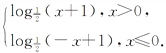
(3)设x1,x2是任意两个值,且x1<x2≤0,
则-x1>-x2≥0,
∴1-x1>1-x2>0.
∵f(x2)-f(x1)=log![]() (-x2+1)-log
(-x2+1)-log![]() (-x1+1)=log
(-x1+1)=log![]()
![]() >log
>log![]() 1=0,
1=0,
∴f(x2)>f(x1),
∴f(x)=log![]() (-x+1)在(-∞,0]上为增函数.
(-x+1)在(-∞,0]上为增函数.
又∵f(x)是定义在R上的偶函数,
∴f(x)在(0,+∞)上为减函数.
∵f(a-1)<-1=f(1),
∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞,0)∪(2,+∞).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
