题目内容
设Sn是正项数列{an}的前n项和,且Sn=
an2+
an-
.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
(1)当n=1时,由条件可得 a1=s1=
+
a1-
,解出a1=3.
(2)又4sn=an2+2an-3①,可得 4sn-1=
+2an-3(n≥2)②,
①-②4an=an2-
+2an-2an-1 ,即
-
-2(an+an-1)=0,
∴(
+an-1)(an-an-1-2)=0,
∵an+an-1>0,∴an-an-1=2(n≥2),
∴数列{an}是以3为首项,2为公差之等差数列,
∴an=3+2(n-1)=2n+1.
(3)由bn=2n,可得Tn=3×21+5×22+…+(2n+1)•2n+0③,
∴2Tn=0+3×22+…+(2n-1)•2n+(2n+1)2n+1④,
④-③可得 Tn=-3×21-2(22+23+…+2n)+(2n+1)2n+1=(2n-1)2n+1+2,
∴Tn=(2n-1)•2n+1+2.
| 1 |
| 4 |
| a | 21 |
| 1 |
| 2 |
| 3 |
| 4 |
(2)又4sn=an2+2an-3①,可得 4sn-1=
| a | 2n-1 |
①-②4an=an2-
| a | 2n-1 |
| a | 2n |
| a | 2n-1 |
∴(
| a | n |
∵an+an-1>0,∴an-an-1=2(n≥2),
∴数列{an}是以3为首项,2为公差之等差数列,
∴an=3+2(n-1)=2n+1.
(3)由bn=2n,可得Tn=3×21+5×22+…+(2n+1)•2n+0③,
∴2Tn=0+3×22+…+(2n-1)•2n+(2n+1)2n+1④,
④-③可得 Tn=-3×21-2(22+23+…+2n)+(2n+1)2n+1=(2n-1)2n+1+2,
∴Tn=(2n-1)•2n+1+2.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
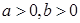 ,且
,且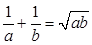 .
.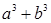 的最小值;
的最小值;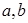 ,使得
,使得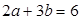 ?并说明理由.
?并说明理由.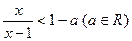
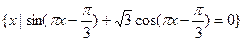 ,若
,若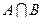 恰有3个元素,求a的取值范围。
恰有3个元素,求a的取值范围。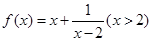 ,在
,在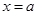 处取最小值,则
处取最小值,则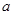 =( )
=( )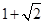
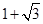
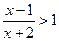 的解集是 。
的解集是 。