题目内容
an=
,sn为其前n项和,则
sn=( )
| n+2 |
| n!+(n+1)!+(n+2)! |
| lim |
| n→∞ |
| A、0 | ||
B、
| ||
C、
| ||
| D、不存在 |
考点:数列的极限,数列的求和
专题:点列、递归数列与数学归纳法
分析:利用n!=1×2×3×…×n,可将an=
化简为:an=
-
,再求和后取其极限即可.
| n+2 |
| n!+(n+1)!+(n+2)! |
| 1 |
| (n+1)! |
| 1 |
| (n+2)! |
解答:
解:∵an=
=
=
=
=
-
,
∴a1+a2+…+an=[(
-
)+(
-
)+…+(
-
)]
=
-
,
∴
sn=
(
-
)=
-
=
-0=
=
.
故选:B.
| n+2 |
| n!+(n+1)!+(n+2)! |
| n+2 |
| n![1+(n+1)+(n+2)(n+1)] |
| n+2 |
| n!(n+2)2 |
| 1 |
| n!(n+2) |
| 1 |
| (n+1)! |
| 1 |
| (n+2)! |
∴a1+a2+…+an=[(
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| 3! |
| 1 |
| 4! |
| 1 |
| (n+1)! |
| 1 |
| (n+2)! |
=
| 1 |
| 2! |
| 1 |
| (n+2)! |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2! |
| 1 |
| (n+2)! |
| 1 |
| 2! |
| lim |
| n→∞ |
| 1 |
| (n+2)! |
| 1 |
| 2! |
| 1 |
| 2! |
| 1 |
| 2 |
故选:B.
点评:本题考查数列的极限,化简an=
-
是关键,考查裂项法求和,突出转化思想的考查.
| 1 |
| (n+1)! |
| 1 |
| (n+2)! |

练习册系列答案
相关题目
已知
和
是两个单位向量,夹角为
,则下面向量中与2
-
垂直的是( )
| e1 |
| e2 |
| π |
| 3 |
| e2 |
| e1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若抛物线y2=2px(p>0)上一点Q到准线和抛物线的对称轴的距离分别为10和6,则此点Q的横坐标为( )
| A、1 | B、9 | C、2 | D、1或9 |
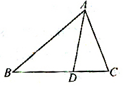 在△ABC中,∠A=60°,且∠A的平分线AD将BC分成两段之比为BD:DC=2:1,又AD=
在△ABC中,∠A=60°,且∠A的平分线AD将BC分成两段之比为BD:DC=2:1,又AD=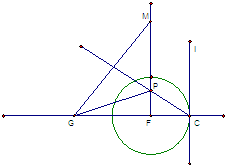 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为