题目内容
4.计算:(1)(0.0081)${\;}^{-\frac{1}{4}}$一[3×($\frac{7}{8}$)0]-1×[81-0.25+($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$]${\;}^{-\frac{1}{2}}$-10×0.027${\;}^{\frac{1}{3}}$;
(2)已知x+y=12,xy=9,且x<y,求$\frac{{x}^{\frac{1}{2}}+{y}^{\frac{1}{2}}}{{x}^{\frac{1}{2}}-{y}^{\frac{1}{2}}}$.
分析 根据指数和对数的运算性质解答即可.
解答 解:(1)原式=[(0.3)${\;}^{4}]^{-\frac{1}{4}}$-${\;}^{\frac{1}{4}}$-$\frac{1}{3}$($\frac{1}{3}$$+\frac{2}{3}$)${\;}^{-\frac{1}{2}}$-10×0.3
=$\frac{10}{3}$-$\frac{1}{3}$-3
=0.
(2)原式=-$\frac{\sqrt{({x}^{\frac{1}{2}}+{y}^{\frac{1}{2}})^{2}}}{\sqrt{({x}^{\frac{1}{2}}-{y}^{\frac{1}{2}})^{2}}}$
=-$\frac{\sqrt{x+y+2•(xy)^{\frac{1}{2}}}}{\sqrt{x+y-2•(xy)^{\frac{1}{2}}}}$
=-$\frac{\sqrt{12+6}}{\sqrt{12-6}}$
=-$\sqrt{3}$
点评 本题主要考查指数运算和对数的运算性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知数列{xn}满足lgxn+1=1+lgxn(n∈N*),且x1+x2+x3+…+x100=100,则lg(x101+x102+…+x200)的值为( )
| A. | 102 | B. | 101 | C. | 100 | D. | 99 |
9.函数f(x)=$\sqrt{x}$-x的单调递减区间为( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{4}$)∪$\frac{1}{2}$,+∞) | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
13.若y=lnx,则其图象在x=2处的切线斜率是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 0 |
14.为了研究“教学方式”对教学质量的影响,某高中英语老师分别用两种不同的教学方法对入学英语平均分和优秀率都相同的甲乙两个高一新班进行教学(勤奋程度和自觉性相同),以下茎叶图为甲乙两班(每班均20人)学生的英语期末成绩,若成绩不低于125分的为优秀,填写下面的2×2列联表,并判断是否有97.5%的把握认为“成绩优秀与教学方式有关”.
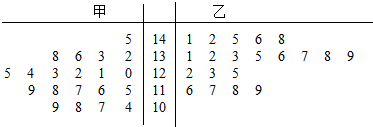
参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{{n}_{+2}}^{\;}}$
附表:

| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
附表:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |