题目内容

19．已知数列{xn}满足lgxn+1=1+lgxn（n∈N*），且x1+x2+x3+…+x100=100，则lg（x101+x102+…+x200）的值为（　　）
A．102B．101C．100D．99

分析 数列{xn}满足lgxn+1=1+lgxn（n∈N*），可得$lg\frac{{x}_{n+1}}{{x}_{n}}$=1，即xn+1=10xn．再利用等比数列的通项公式及其性质即可得出．

解答 解：∵数列{xn}满足lgxn+1=1+lgxn（n∈N*），
∴$lg\frac{{x}_{n+1}}{{x}_{n}}$=1，即xn+1=10xn．
∴数列{xn}是公比为10的等比数列．
且x1+x2+x3+…+x100=100，
则lg（x101+x102+…+x200）lg10100（x1+x2+…+x100）=lg10100•100=102．
故选：A．

点评 本题考查了等比数列的通项公式及其性质、对数的运算性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
9．如图，在矩形 OABC中，$\overrightarrow{{A}{B}}=3\overrightarrow{{A}{E}}$，$\overrightarrow{{B}C}=3\overrightarrow{FC}$，若$\overrightarrow{{O}{B}}=λ\overrightarrow{{O}{E}}+μ\overrightarrow{{O}F}$（λ，μ∈R），则λμ等于（　　）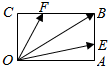
A．$\frac{9}{4}$B．$\frac{9}{16}$C．$\frac{4}{9}$D．$\frac{16}{9}$
10．已知下列命题：①若$\overrightarrow{a}•\overrightarrow{b}$＜0，则$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为钝角；②a，b∈C，则“ab∈R”是“a，b互为共轭复数”的必要非充分条件；③一个骰子连续投2次，点数和为4的概率为$\frac{1}{9}$；④若n为正奇数，则6n+${C}_{n}^{1}{6}^{n-1}$+${C}_{n}^{2}{6}^{n-2}$+…+${C}_{n}^{n-1}6-1$被8除的余数是5，其中正确的序号是②④．
7．已知f（x）=log2x，则f-1（x）满足（　　）
A．f-1（2x）=2f-1（x）B．f-1（2x）=$\frac{1}{2}$f-1（x）C．f-1（2x）=[f-1（x）]2D．f-1（2x）=[f-1（x）]${\;}^{\frac{1}{2}}$
14．已知数列{an}的前n项和${S_n}={n^2}$，则a5的值为（　　）
A．9B．11C．15D．25
4．计算：
（1）（0.0081）${\;}^{-\frac{1}{4}}$一[3×（$\frac{7}{8}$）0]-1×[81-0.25+（$\frac{27}{8}$）${\;}^{-\frac{1}{3}}$]${\;}^{-\frac{1}{2}}$-10×0.027${\;}^{\frac{1}{3}}$；
（2）已知x+y=12，xy=9，且x＜y，求$\frac{{x}^{\frac{1}{2}}+{y}^{\frac{1}{2}}}{{x}^{\frac{1}{2}}-{y}^{\frac{1}{2}}}$．
11．已知函数f（x）=$\frac{2}{3}$x3-2ax2-3x（a∈R），若曲线y=f（x）在点P（1，f（1））处的切线与直线x+3y+1=0垂直，则实数a的值为（　　）
A．-1B．1C．-$\frac{1}{6}$D．$\frac{1}{6}$
8．用max{a，b，c}表示a，b，c三个数中的最大值，设f（x）=max{2x，x+2，10-x}（x≥0），则f（x）取得最小值时x所在区间为（　　）
A．（1，2）B．（2，3）C．（3，4）D．（4，5）
9．下列说法正确的是（　　）
A．从独立性检验可知有99%的把握认为吃地沟油与患肠胃癌有关系时，我们说某人吃地沟油，那么他有99%的可能患肠胃癌
B．回归直线不一定过样本中心点（$\overline{x}$，$\overline{y}$）
C．相关系数-1≤r≤1．r越大，线性相关的关系越强
D．用样本研究变量间的相关关系，求得回归直线方程为y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，回归系数为r，若$\stackrel{∧}{b}$＞0，则r＞0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网