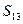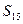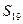题目内容
数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负.
(1)求数列的公差;
(2)求前n项和Sn的最大值;
(3)当Sn>0时,求n的最大值.
(1)求数列的公差;
(2)求前n项和Sn的最大值;
(3)当Sn>0时,求n的最大值.
(1)d=-4;(2)S6=6×23+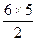 (-4)=78;(3)n的最大值为12。
(-4)=78;(3)n的最大值为12。
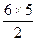 (-4)=78;(3)n的最大值为12。
(-4)=78;(3)n的最大值为12。(1)由已知a6=a1+5d=23+5d>0,a7=a1+6d=23+6d<0,
解得:-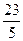 <d<-
<d<-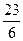 ,又d∈Z,∴d=-4
,又d∈Z,∴d=-4
(2)∵d<0,∴{an}是递减数列,又a6>0,a7<0
∴当n=6时,Sn取得最大值,S6=6×23+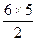 (-4)=78
(-4)=78
(3)Sn=23n+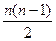 (-4)>0,整理得:n(50-4n)>0
(-4)>0,整理得:n(50-4n)>0
∴0<n<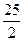 ,又n∈N*,
,又n∈N*,
所求n的最大值为12.
解得:-
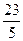 <d<-
<d<-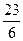 ,又d∈Z,∴d=-4
,又d∈Z,∴d=-4(2)∵d<0,∴{an}是递减数列,又a6>0,a7<0
∴当n=6时,Sn取得最大值,S6=6×23+
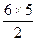 (-4)=78
(-4)=78(3)Sn=23n+
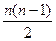 (-4)>0,整理得:n(50-4n)>0
(-4)>0,整理得:n(50-4n)>0∴0<n<
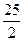 ,又n∈N*,
,又n∈N*,所求n的最大值为12.

练习册系列答案
相关题目
 ,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设
,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设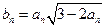 ,证明bn<bn+1,其中n为正整数.
,证明bn<bn+1,其中n为正整数.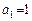 ,
,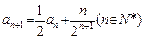 .
.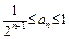
 ,且
,且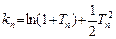 ,证明:
,证明: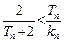 .
.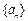 中,
中,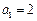 ,对于任意的
,对于任意的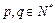 ,有
,有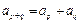
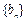 满足:
满足: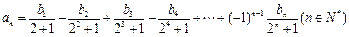 求数列
求数列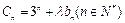 ,是否存在实数
,是否存在实数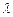 ,当
,当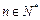 时,
时,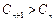 恒成立,若存在,求实数
恒成立,若存在,求实数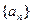 中,
中,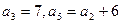 ,则
,则 。
。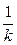 ,ak=
,ak=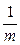 ,则该数列前mk项之和是 .
,则该数列前mk项之和是 .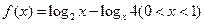 ,数列
,数列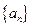 的通项
的通项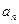 满足
满足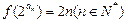 .
. 的前
的前 项和为
项和为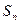 ,且
,且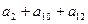 为一确定的常数,则下列各式中,也为确定的常数的是 ( )
为一确定的常数,则下列各式中,也为确定的常数的是 ( )