题目内容
【题目】在某大型活动中，甲、乙等五名志愿者被随机地分到A，B，C，D四个不同的岗位服务，每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率；
(2)求甲、乙两人不在同一个岗位服务的概率；
(3)求五名志愿者中仅有一人参加A岗位服务的概率.
【答案】(1)
(2)
(3) 
【解析】
（1）甲、乙两人同时参加A岗位服务，则另外三个人在B、C、D三个位置进行全排列，所有的事件数是从5个人中选2个作为一组，同其他3人共4个元素在四个位置进行排列；
（2）总事件数同第一问一样，甲、乙两人不在同一个岗位服务的对立事件是甲、乙两人同时参加同一岗位服务，即甲、乙两人作为一个元素同其他三个元素进行全排列；
（3）先求出有两人同时参加A岗位服务的概率,然后用1去减即可.
(1)记“甲、乙两人同时参加A岗位服务”为事件EA，那么
，
即甲、乙两人同时参加A岗位服务的概率是；
(2)记“甲、乙两人同时参加同一岗位服务”为事件E，那么
，所以甲、乙两人不在同一岗位服务的概率是P(
)＝1－P(E)＝；
(3)因为有两人同时参加A岗位服务的概率
，所以仅有一人参加A岗位服务的概率P1＝1－P2＝.
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”，彰显出中国式创新的强劲活力．某移动支付公司从某市移动支付用户中随机抽取100人进行调查，得到如下数据：
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 |
（1）把每周使用移动支付6次及以上的用户称为“移动支付达人”，按分层抽样的方法，从参与调查的“移动支付达人”中，随机抽取6人，求抽取的6人中，男、女用户各多少人；
（2）把每周使用移动支付超过3次的用户称为“移动支付活跃用户”，根据表格中的数据完成下列
列联表，问：能否有
的把握认为“移动支付活跃用户”与性别有关？
非移动支付活跃用户 | 移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 |
附参照表：
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式：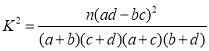
，其中
