题目内容
【题目】在平面中，△ABC的角C的内角平分线CE分△ABC面积所成的比 
= 
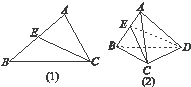
．将这个结论类比到空间：在三棱锥A﹣BCD中，平面DEC平分二面角A﹣CD﹣B且与AB交于E，则类比的结论为 
= ． 
【答案】
?= 
【解析】解：在平面中△ABC的角C的内角平分线CE分△ABC面积所成的比 
= 
，
将这个结论类比到空间：在三棱锥A﹣BCD中，平面DEC平分二面角A﹣CD﹣B且与AB交于E，
则类比的结论为根据面积类比体积，长度类比面积可得： = ，
所以答案是： = ．
【考点精析】认真审题，首先需要了解类比推理(根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理)．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】自2016年1月1日起，我国全面二孩政策正式实施，这次人口与生育政策的历史性调整，使得“要不要再生一个”，“生二孩能休多久产假”等问题成为千千万万个家庭在生育决策上避不开的话题．为了解针对产假的不同安排方案形成的生育意愿，某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查，得到如下数据：
产假安排（单位：周） | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
（1）若用表中数据所得的频率代替概率，面对产假为14周与16周，估计某家庭有生育意愿的概率分别为多少？
（2）假设从5种不同安排方案中，随机抽取2种不同安排分别作为备选方案，然后由单位根据单位情况自主选择．
①求两种安排方案休假周数和不低于32周的概率；
②如果用
表示两种方案休假周数之和．求随机变量
的分布列及数学期望．
